Wolfram Demonstrations Project

11,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

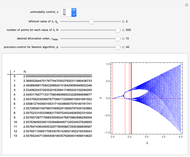
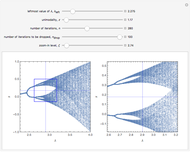
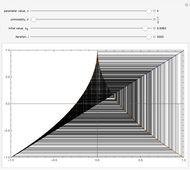
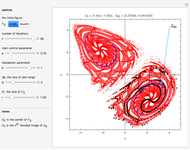
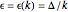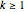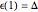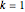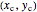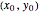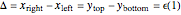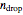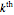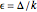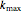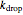Box-Counting Algorithm of the Hénon Map

Download to Desktop Copy to Clipboard
Source

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram CDF Player or other Wolfram Language products.

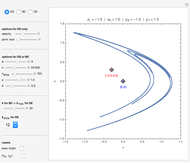
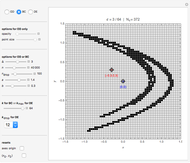
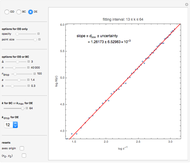
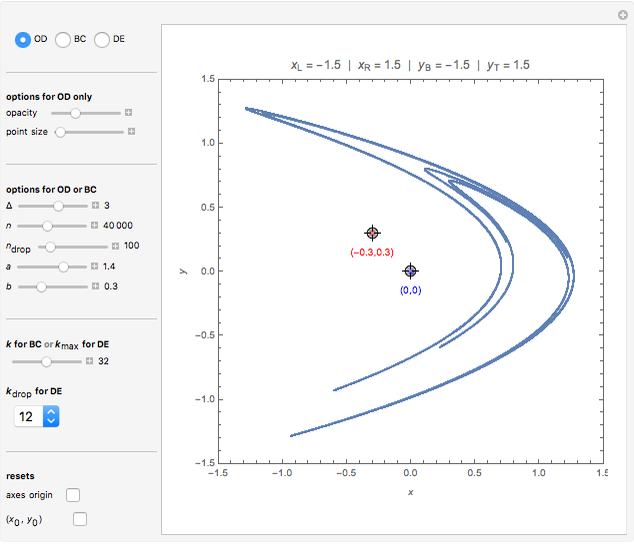
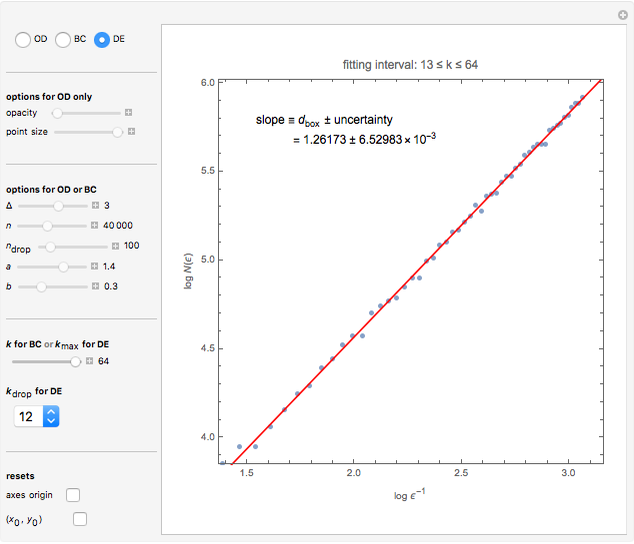
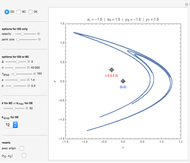
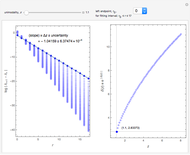
Requires a Wolfram Notebook System

Edit on desktop, mobile and cloud with any Wolfram Language product.

This Demonstration shows the orbit diagram (OD), the box counting diagram (BC), and the dimension estimation plot (DE) of the Hénon map 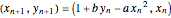[1–4]. It is known that the chaotic attractors in the Hénon map are neither area filling (dimension 2) nor a simple curve (of dimension 1) [4]. Therefore the dimensions of these complicated geometries must be non-integer values between 1 and 2, and the chaotic attractors are then called fractals or strange attractors [4, 5]. The capacity or box-counting dimension 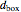is the simplest possible way to measure such pathologies. It can be defined by

[more]

,

where is the number of boxes with size covering the attractor [5–7]. Here is the box-counting step and is the size of the box at the initial step .

• Drag the blue locator to change the position of the center .

• Drag the red locator to change the initial condition .

The sliders let you control the following:

• opacity, the opacity of the plotted points.

• point size, the size of the plotted points.

• , the sizes of the horizontal and vertical plot range; .

• , the number of iterations.

• , the number of initial iterations to be dropped.

• , the main control parameter value.

• , the dissipation parameter value.

• , the box-counting step; the size of the boxes at the box-counting step is given by .

• , the maximum box-counting step.

The dropdown menu lets you control:

• , the number of initial box-counting steps to be dropped.

And, finally, the resets let you reset the position of the locators.

[less]

Contributed by: Ki-Jung Moon (January 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

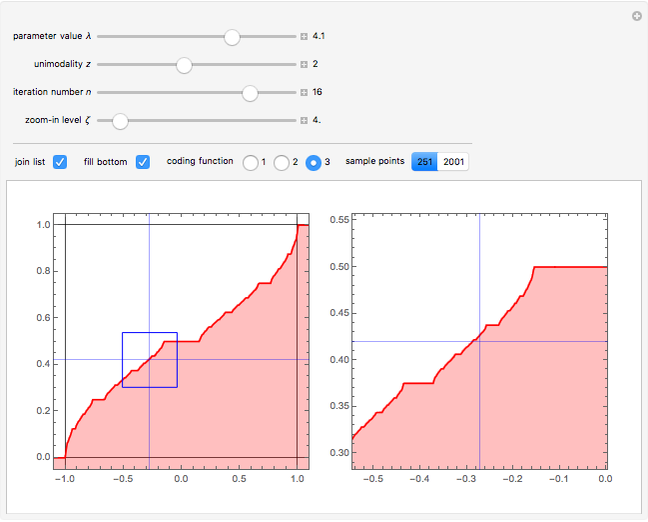
The original Hénon map, which is given by 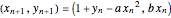, is a prototypical example of a two-dimensional dissipative map with chaotic behavior. It was proposed by M. Hénon in 1976 as a simplified model of the Poincaré map (or Poincaré section) for the Lorenz model [1,8]. Hénon showed that the chaotic attractor of the Hénon map with 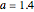and 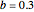(also called the Hénon attractor) exhibits strange behavior (self-similarity), the typical behavior of fractal sets, via successive enlargement of the local region of the orbit diagram. Therefore the Hénon attractor is not only chaotic but also strange. These "Hénon-like" attractors are widely distributed within the parameter range 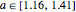and 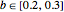. They can also be found in other parameter regions. The maximally chaotic attractor for the Hénon map is known to occur at and [9]. This Demonstration uses an alternative definition of the Hénon map 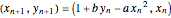with the same dynamics [9].

References

[1] M. Hénon, "A Two-Dimensional Mapping with a Strange Attractor," Communications in Mathematical Physics, 50(1), 1976 pp. 69–77.

[2] S. H. Strogatz, Nonlinear Dynamics and Chaos, New York: Perseus Books Publishing, 1994.

[3] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.

[4] H.-O. Peitgen, H. Jurgens, and D. Saupe, Chaos and Fractals: New Frontiers of Science, 2nd ed., New York: Springer, 2004.

[5] B. Mandelbrot, The Fractal Geometry of Nature, San Francisco: W. H. Freeman, 1982.

[6] D. A. Russel, J. D. Hanson, and E. Ott, "Dimension of Strange Attractor," Physical Review Letters, 45(14), 1980 p. 1175.

[7] P. Grassberger and I. Procaccia, "Measuring the Strangeness of Strange Attractors," Physica, 9D(1–2), 1983 pp. 189–208.

[8] E. N. Lorenz, "Deterministic Nonperiodic Flow," Journal of the Atmospheric Sciences, 20(2), 1963 pp. 130-141.

[9] J. C. Sprott, "Maximally Complex Simple Attractors," Chaos: An Interdisciplinary Journal of Nonlinear Science, 17, 2007 p. 033124.

Embed Code

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send