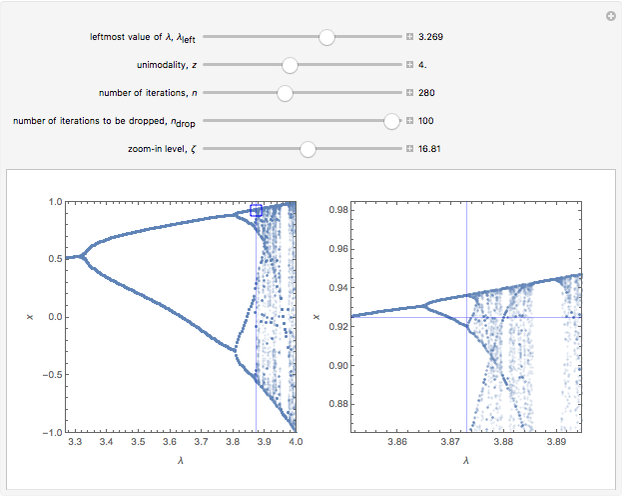
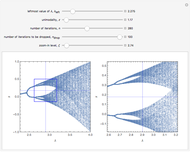
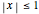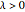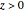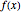Bifurcation Diagram for a Generalized Logistic Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
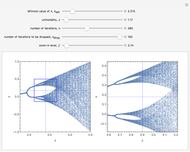
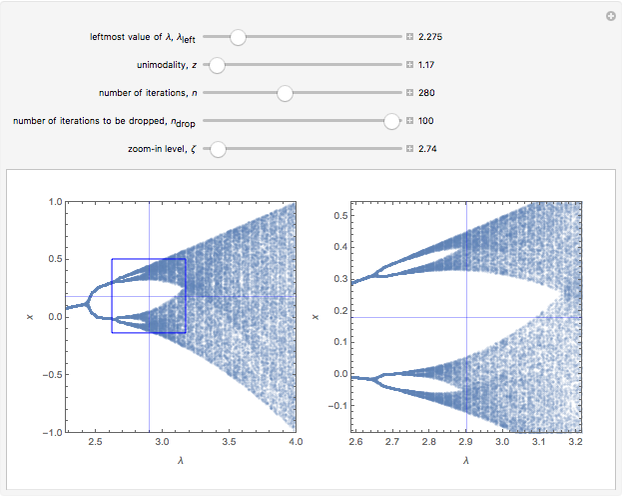
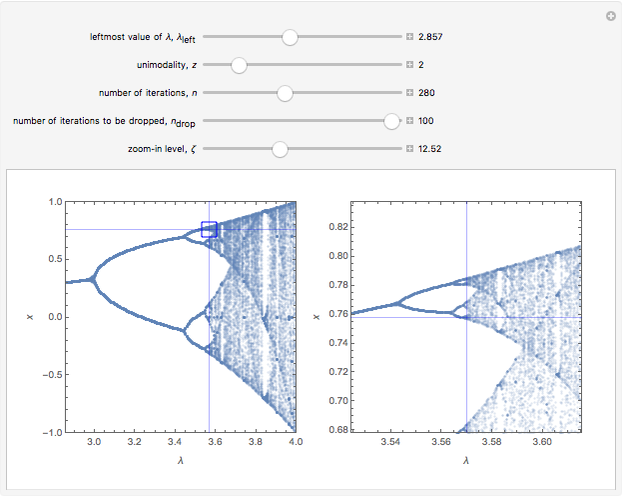
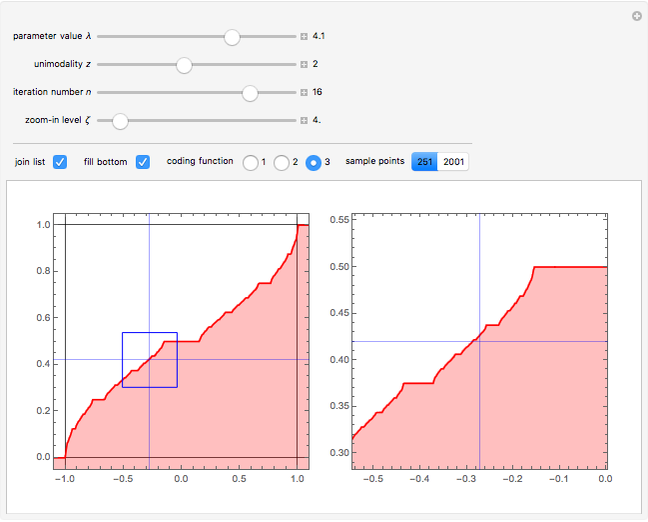
This Demonstration shows a bifurcation diagram for a generalized logistic map, 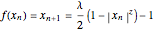 [1–7]. This map is very well-suited for numerical analysis because:
[1–7]. This map is very well-suited for numerical analysis because:
Contributed by: Ki-Jung Moon (October 2013)
Based on programs by: Ed Pegg Jr, Enrique Zeleny, C. Pellicer-Lostao, and R. Lopez-Ruiz
Open content licensed under CC BY-NC-SA
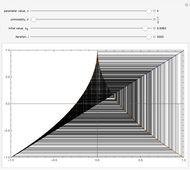
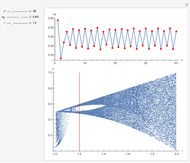
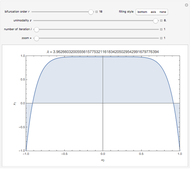
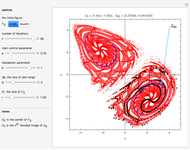
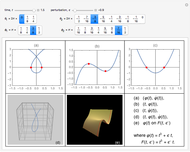
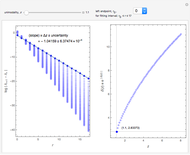
Snapshots
Details
• The test map generalizes the well-known logistic map [1–5].
• The initial condition 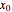 is fixed at
is fixed at  .
.
• For 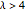 or for
or for 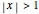 , the iterates of
, the iterates of 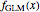 rapidly approach
rapidly approach 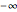 (more rapidly for larger values of
(more rapidly for larger values of 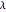 and
and  ) and therefore, due to the finite length in precision, the numbers are too large to compute [8]. A little trick is used to avoid this problem.
) and therefore, due to the finite length in precision, the numbers are too large to compute [8]. A little trick is used to avoid this problem.
References
[1] S. H. Strogatz, Nonlinear Dynamics and Chaos, New York: Perseus Books Publishing, 1994.
[2] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.
[3] H.-O. Peitgen, H. Jurgens, and D. Saupe, Chaos and Fractals: New Frontiers of Science, 2nd ed., New York: Springer, 2004.
[4] M. J. Feigenbaum, "Quantitative Universality for a Class of Nonlinear Transformations," Journal of Statistical Physics, 19(1), 1978 pp. 25–52. doi:10.1007/BF01020332.
[5] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21(6), 1979 pp. 669–706. doi:10.1007/BF01107909.
[6] K.-J. Moon and S. D. Choi, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18(2), 2008 pp. 023104. doi:10.1063/1.2902826.
[7] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010 pp. 049902. doi:10.1063/1.3530128.
[8] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.
Permanent Citation