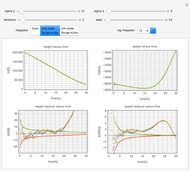
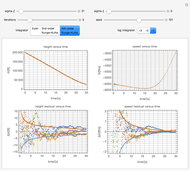
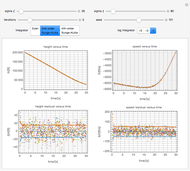
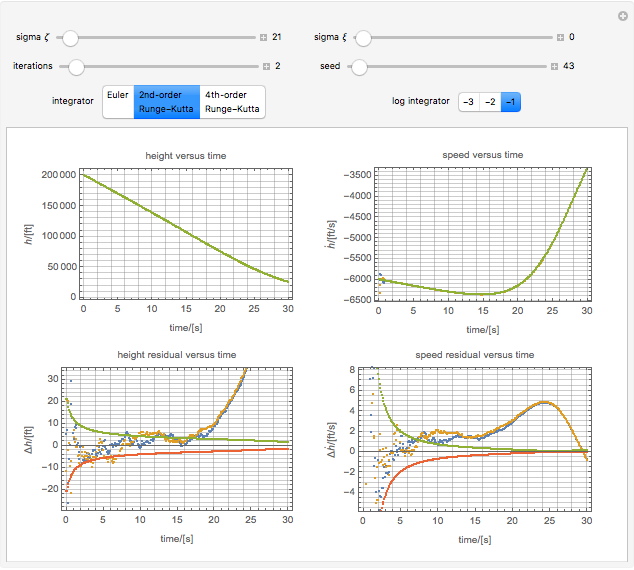
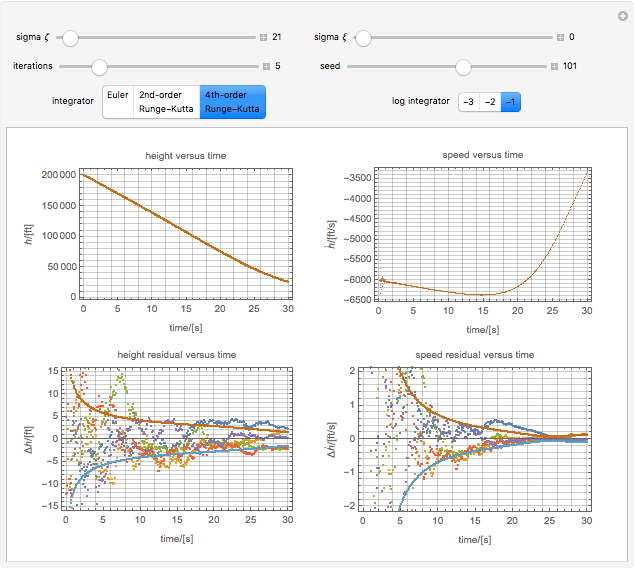
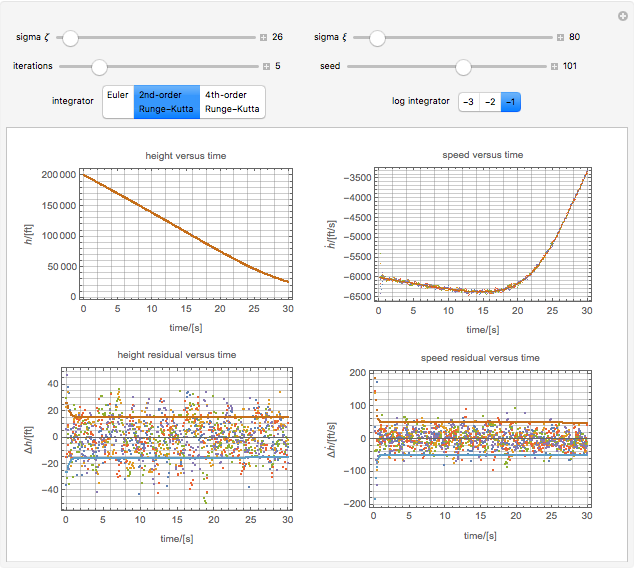
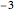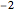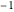Tuning an Extended Kalman Filter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Kalman filter is an algorithm that seeks to find the optimal representation for a series of observations by averaging over successive states, a type of Bayesian model. In its simplest form, it exploits the mathematical fact that the product of two Gaussians is another Gaussian.
[more]
Contributed by: Brian C. Beckman (May 2016)
Open content licensed under CC BY-NC-SA
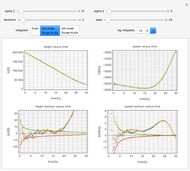
Snapshots
Details
The example uses advanced functional programming over lazy streams to integrate in constant memory and to modularize the integrators and other components. The code has many reusable parts and is worthy of study independently of the application to Kalman filtering.
Reference
[1] P. Zarchan and H. Musoff, Fundamentals of Kalman Filtering: A Practical Approach, 4th ed., Reston, VA: American Institute of Aeronautics and Astronautics, 2015 Chapter 7. doi:10.2514/4.102776.
Permanent Citation
"Tuning an Extended Kalman Filter"
http://demonstrations.wolfram.com/TuningAnExtendedKalmanFilter/
Wolfram Demonstrations Project
Published: May 31 2016