Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Understanding Braids and Knots

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

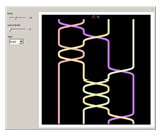
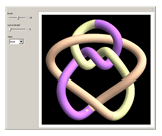
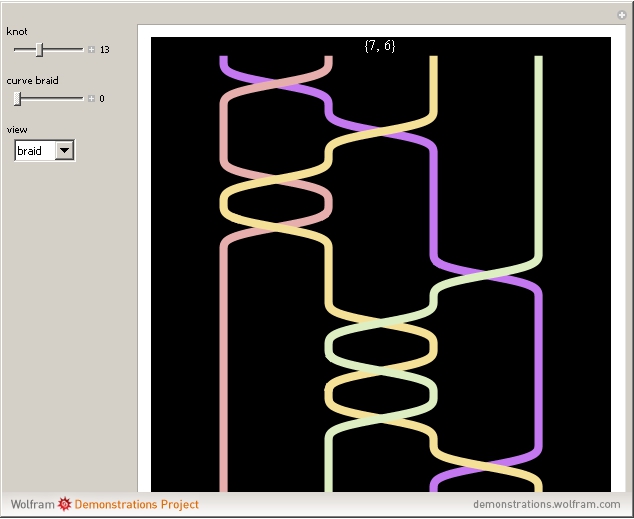
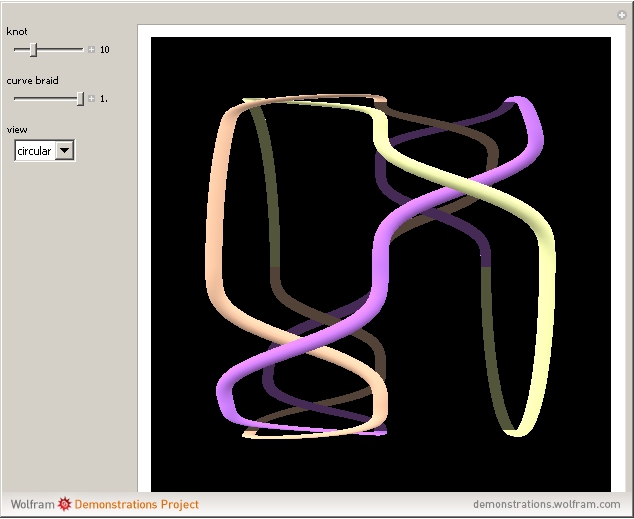
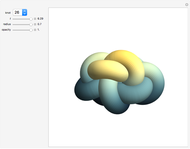
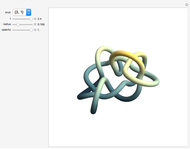
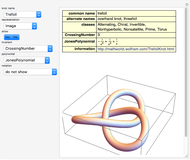
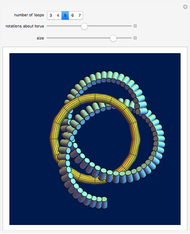
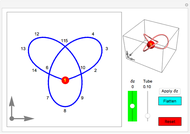
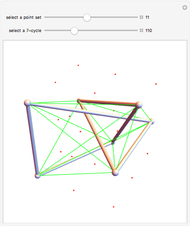
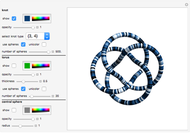
A knot is an interwoven, closed, non-self-intersecting curve in 3D. A braid is a collection of strands crossing over or under each other. By joining the endpoints at the top of the braid diagram to the corresponding endpoints at the bottom, a braid can be associated with a knot. To do this, use the "curve braid" control.

[more]

In this Demonstration, the strands of a braid are plotted with different colors, which are carried over to the corresponding knot. The indices for the braids represent the number of crossings and how the corresponding knot can be tied.

[less]

Contributed by: Enrique Zeleny (September 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] The Knot Atlas. (Aug 28, 2014) katlas.math.toronto.edu/wiki/Main_Page.

[2] E. Dalvit. "A Journey through the Mathematical Theory of Braids." (Aug 28, 2014) matematita.science.unitn.it/braids/index.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send