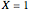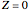Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Unsteady-State Evaporation in an Infinite Tube

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

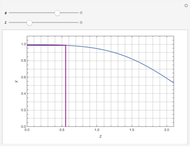
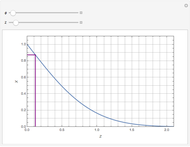
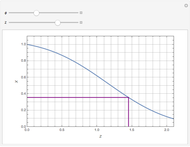
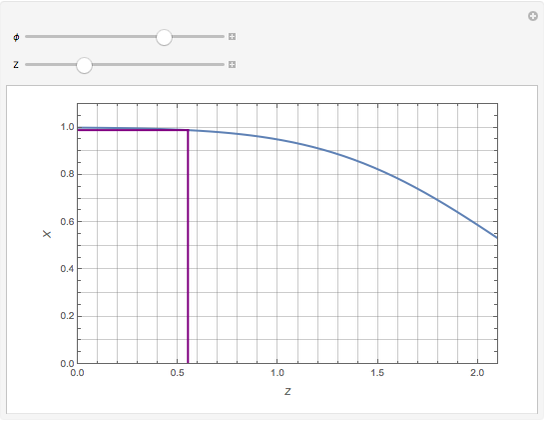
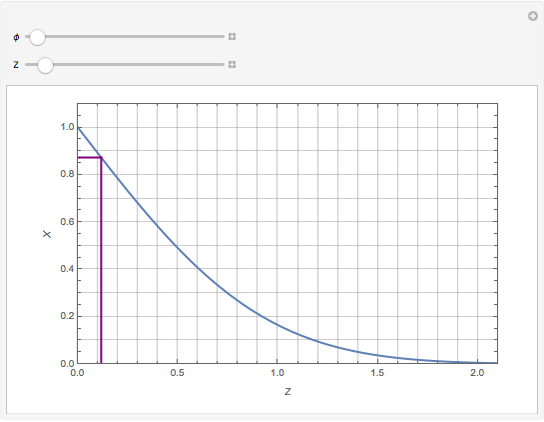
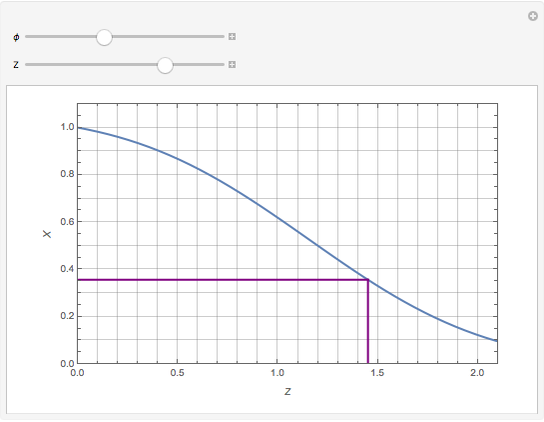
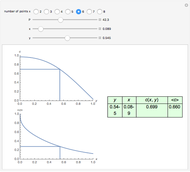
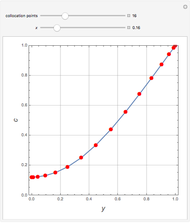
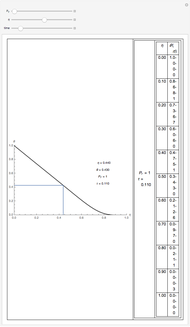
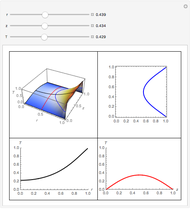
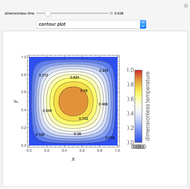
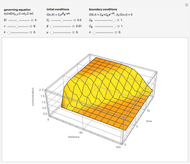
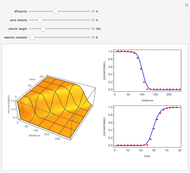
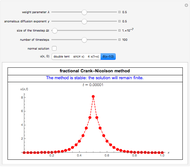
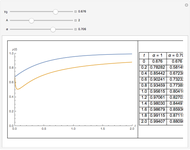
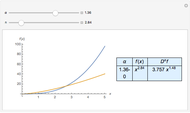
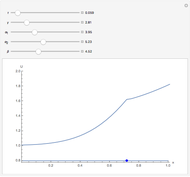
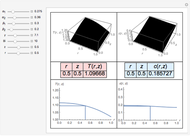
This Demonstration shows the unsteady-state evaporation of a liquid in bulk of vapor in an infinite tube, as governed by the following equation:

[more]

,

with

, .

Here is the diffusion coefficient, is the time, is the mole fraction of compound in the gaseous phase, is the nondimensional media molar velocity, and is the vertical position in the tube.

The boundary conditions are

at ,

at .

The problem is solved here using a shooting technique.

[less]

Contributed by: Jorge Gamaliel Frade Chávez (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley and Sons.

D. S. Sophianopoulos and P. G. Asteris, "Interpolation Based Numerical Procedure for Solving Two-Point Nonlinear Boundary Value Problems," International Journal of Nonlinear Sciences and Numerical Simulations, 5(1), 2004 pp. 67–78.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send