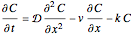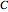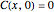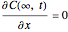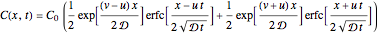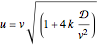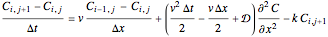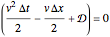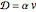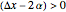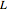Mixing-Cell Model for the Diffusion-Advection Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
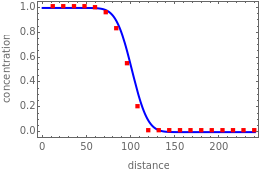
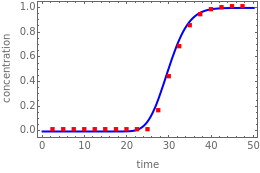
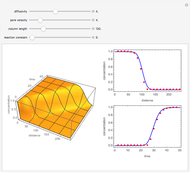
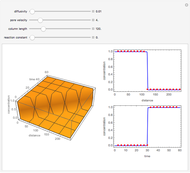
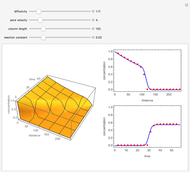
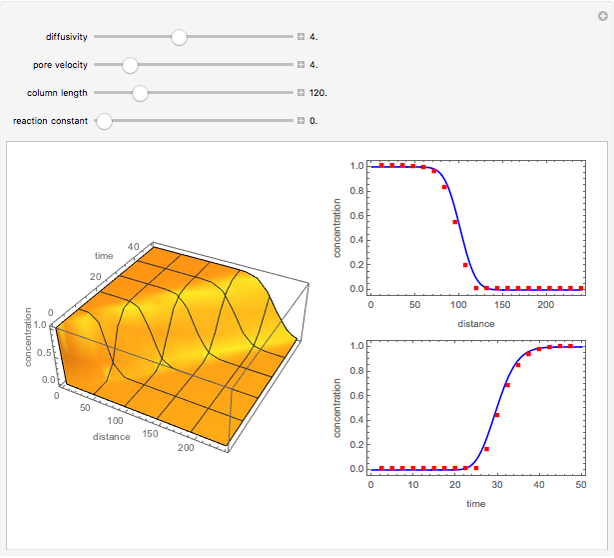
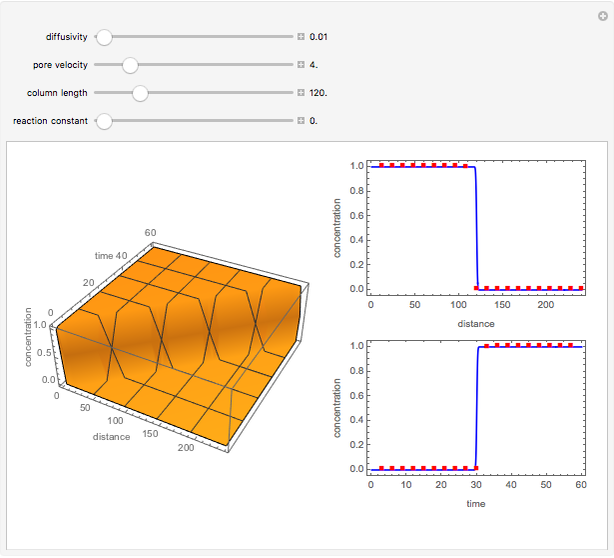
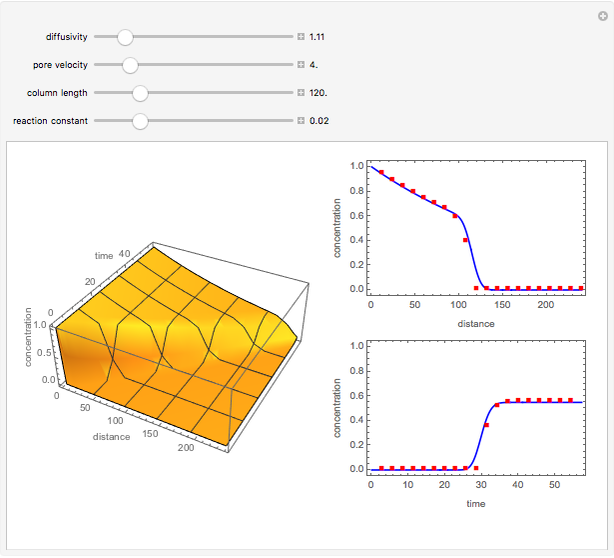
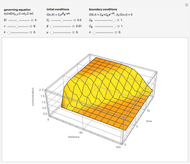
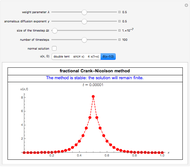
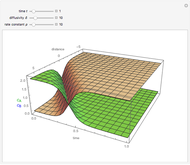
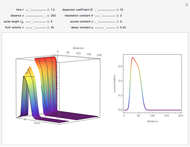
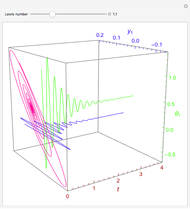
The unsteady-state advection-diffusion equation is solved with a mixing-cell model. The results obtained with this simple model are in excellent agreement with the analytical solution when the correct choice of time and space steps is made. The equation describing the one-dimensional transport of a reactive component in porous media is:
[more]
Contributed by: Clay Gruesbeck (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] M. Th. van Genuchten and W. J. Alves, "Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation," US Department of Agriculture, Technical Bulletin No. 1661, 1982. www.ars.usda.gov/sp2UserFiles/Place/20360500/pdf_pubs/P0753.pdf.
[2] H. C. Van Ommen, "The 'Mixing-Cell' Concept Applied to Transport of Non-reactive and Reactive Components in Soils and Groundwater," Journal of Hydrology, 78(3–4), 1985 pp. 201–213. doi:10.1016/0022-1694(85)90101-5.
Permanent Citation