Viète's Nested Square Root Representation of Pi

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
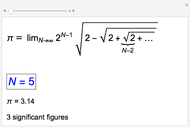
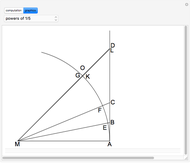
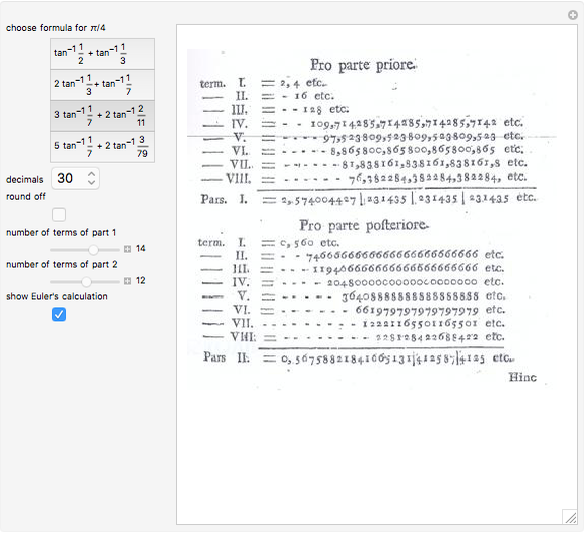
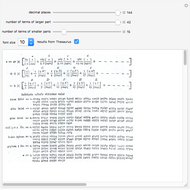
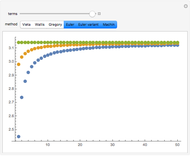
Viète in 1543 derived a representation for  involving a sequence of nested square roots. The formula is displayed in the graphic. The underbrace signifies that the expression above it contains
involving a sequence of nested square roots. The formula is displayed in the graphic. The underbrace signifies that the expression above it contains 
 square roots. For finite values of
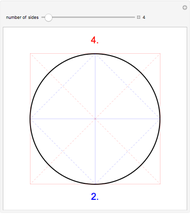
square roots. For finite values of  , the formula represents the perimeter of a regular polygon of
, the formula represents the perimeter of a regular polygon of  sides inscribed in a circle of unit diameter. For a 1024-sided polygon, corresponding to
sides inscribed in a circle of unit diameter. For a 1024-sided polygon, corresponding to  , Viète computed the value
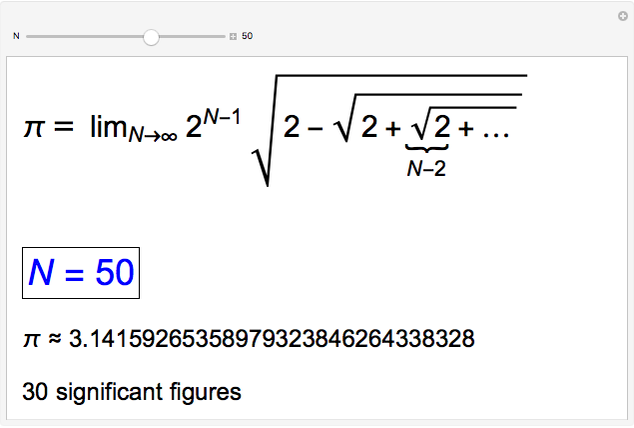
, Viète computed the value  , accurate to 6 significant figures. This Demonstration allows you to extend the result up to
, accurate to 6 significant figures. This Demonstration allows you to extend the result up to  . The capability of Mathematica to compute multiply nested functions is exploited. With
. The capability of Mathematica to compute multiply nested functions is exploited. With  , the underbraced form can be computed using Nest[
, the underbraced form can be computed using Nest[ ,
, ,
,  ].
].
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Viète's Nested Square Root Representation of Pi"
http://demonstrations.wolfram.com/VietesNestedSquareRootRepresentationOfPi/
Wolfram Demonstrations Project
Published: March 7 2011