Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

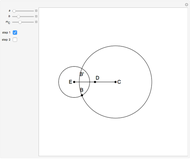
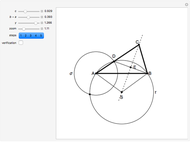
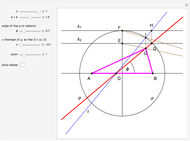
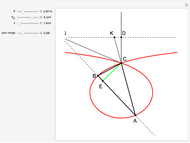
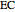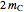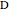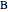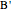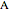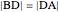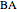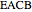15. Construct a Triangle Given the Lengths of Two Sides and the Median to the Third Side

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

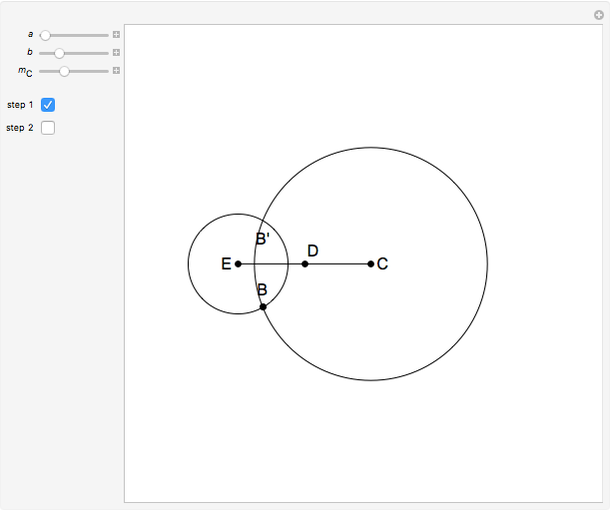
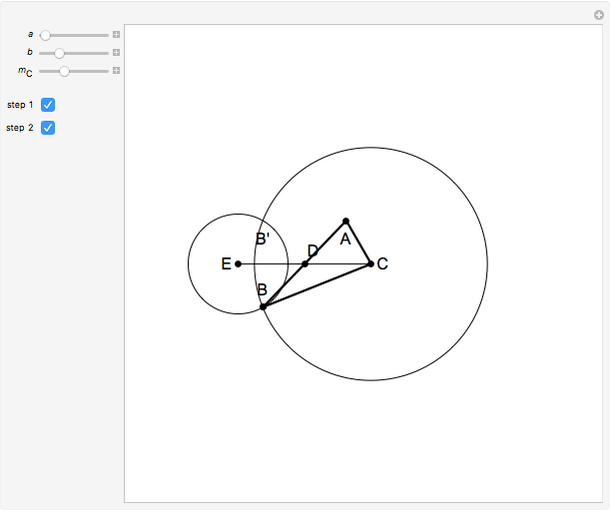
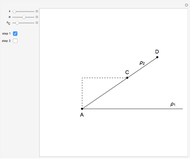
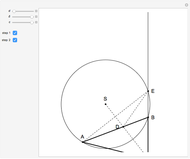
This Demonstration shows a construction of a triangle 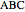given the lengths and of the sides 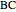and 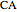and the length of the median 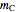from to .

[more]

Construction

Let be a line segment of length and midpoint .

Step 1: Draw a circle with center and radius and a circle with center and radius . Let and be the intersections of the two circles.

Step 2: Extend to the point such that .

Verification

The triangle has side of length .

and bisect each other, so is a parallelogram with sides and . The side has length , and the line segment is the median from of length .

[less]

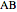Contributed by: Izidor Hafner (August 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

With the condition , the problem has a solution if and only if [1, pp. 287–288].

Reference

[1] A. McFarland, J. McFarland and J. T. Smith, eds., Alfred Tarski: Early Work in Poland: Geometry and Teaching, New York: Birkhäuser, 2014.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send