Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

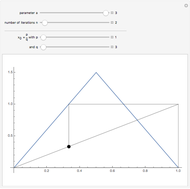
A Convergent Sequence Satisfies the Cauchy Criterion

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

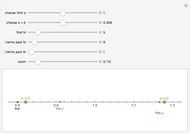
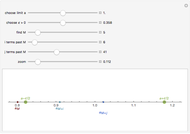
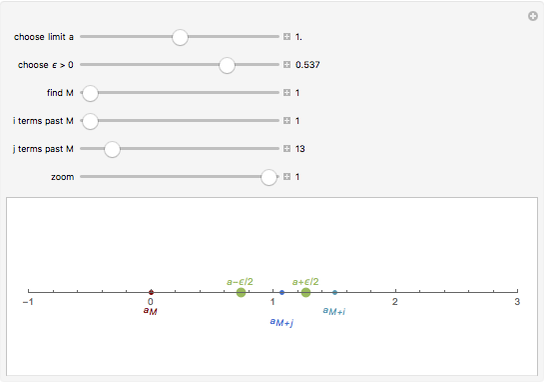
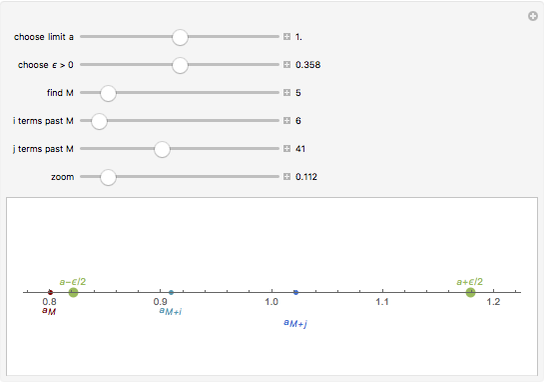
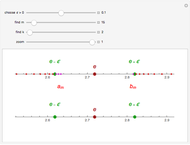
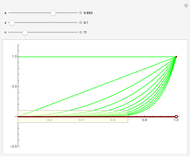
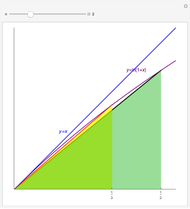
This Demonstration shows that a convergent sequence satisfies the Cauchy criterion. Suppose 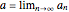. For each , there exists 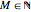, such that for all 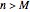, 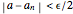. If 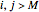, then .

Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

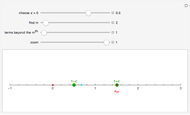
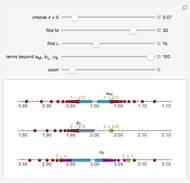
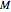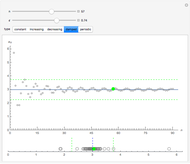
A sequence satisfies the Cauchy criterion if for any , there is a natural number such that for any , |. A metric space is said to be complete if every Cauchy sequence converges. As this Demonstration illustrates, the real numbers are a complete metric space.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send