Action of a 2x2 Singular Transformation Matrix in 2D
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
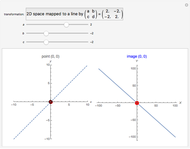
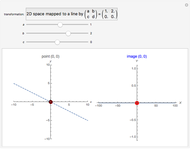
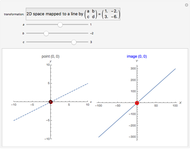
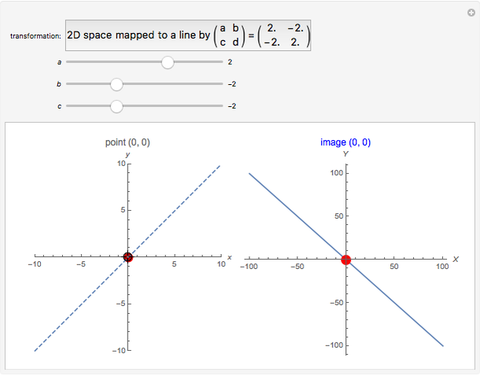
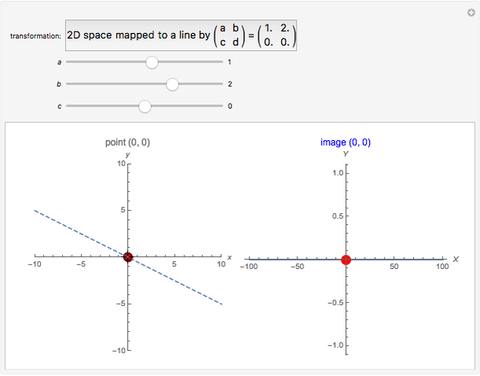
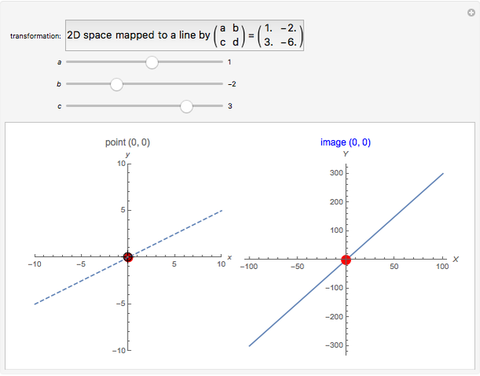
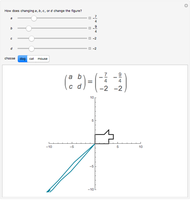
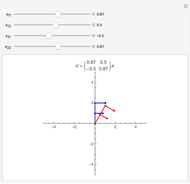
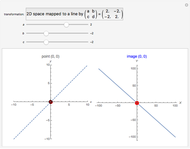
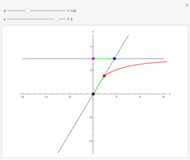
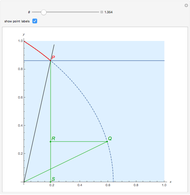
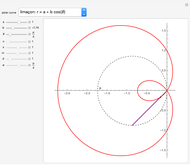
This Demonstration shows the action of 
singular transformation matrices in 2D: all points are either mapped to a line passing through the origin or, if the matrix is null, to the origin itself. Use the sliders to vary three of the elements of the singular matrix.
Contributed by: Roberta Grech (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Transformation matrices are studied in pure math courses by high-school students in some countries.
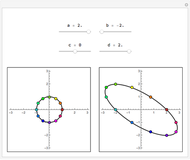
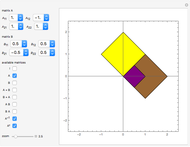
Snapshots 1 and 2: in the case of singular transformation matrices whose entries are not all zero, each point on the image line is the image of infinitely many points—those points on the dashed line in the plot on the left
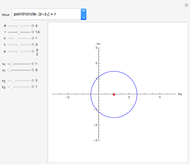
Snapshot 3: in the case of the singular transformation matrix whose entries are all zero, each point in the plot on the left is mapped to the origin
References
[1] L. Bostock, S. Chandler and C. Rourke, Further Pure Mathematics, London, UK: Nelson Thornes, 1982.
[2] C. Berry, T. Heard and D. Martin, MEI AS Further Pure Mathematics, 3rd ed., London: Hodder Education, 2004 pp. 33–34.
Permanent Citation
Effect of a 3x3 Singular Transformation Matrix on 3D Space
Roberta Grech
Matrix Transformation
Michael Ford
Graphical Construction of a 2x2 Matrix and Its Inverse
Jodie Hoh
2x2 Matrix Operations Acting on a Unit Square
Hamide Dogan
Coordinate Transformation of a-Matrix and alpha-Matrix
Robert McIntosh
Change the Dog: Matrix Transformations
Lori Johnson Morse
Matrix Transformations: "F"
Phil Ramsden
Singular Value Decomposition
Chris Maes
Matrix Transpose
Udo Lorz
Sylvester Matrix
Izidor Hafner
-
Action of a 2x2 Singular Transformation Matrix in 2D
Roberta Grech -
Minimizing the Perimeter of a Sector with Given Area
Roberta Grech -
Generating 9-Flips
Roberta Grech -
Solution of Some Second-Order Differential Equations with Constant Coefficients
Roberta Grech -
Convergence of the Binomial Series
Roberta Grech -
Triple Vector Product
Roberta Grech -
The Kappa Curve as a Locus
Roberta Grech -
The Trisectrix as the Locus of Points of Intersection
Roberta Grech -
Effect of a 3x3 Singular Transformation Matrix on 3D Space
Roberta Grech -
Maximizing the Volume of a Right Circular Cone with Given Slant Length
Roberta Grech -
Limaçons as Loci and Other Polar Curves
Roberta Grech -
Series with Interval of Convergence Dependent on Structure
Roberta Grech -
Loci in the Argand Diagram
Roberta Grech