Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

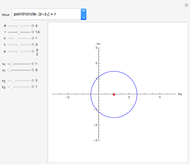
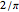The Trisectrix as the Locus of Points of Intersection

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

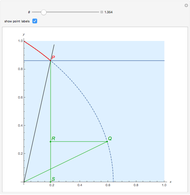
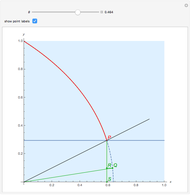
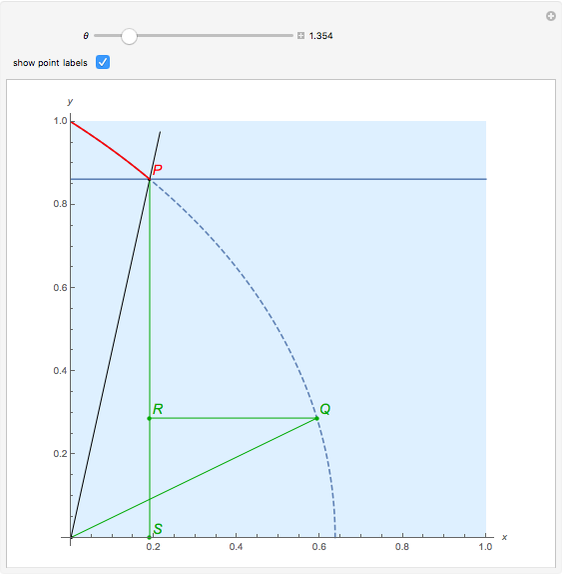
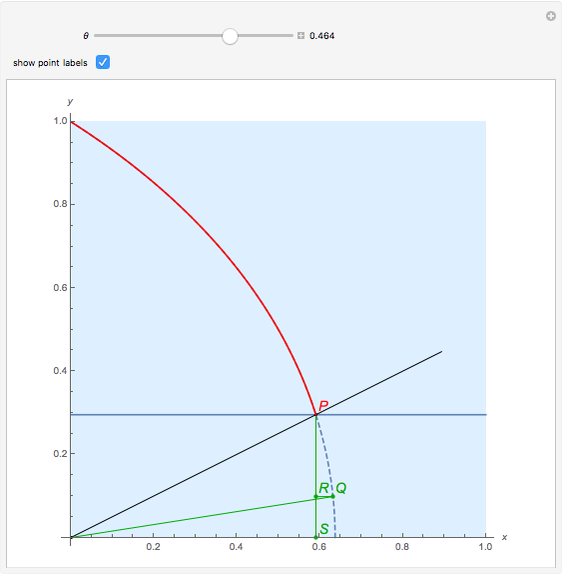
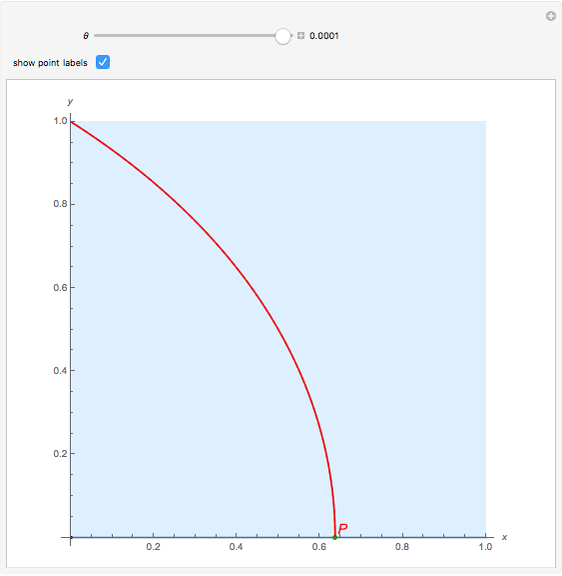
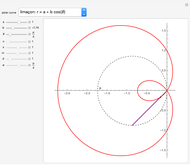
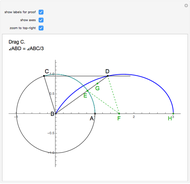
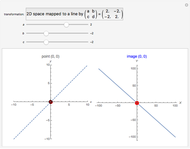
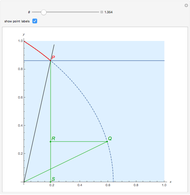
A trisectrix (red) is the locus of the points of intersection (red point 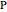) of a moving horizontal line 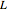(blue) and a rotating line 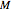(black).

[more]

Initially, the line lies along the line and the line lies along the line . The line rotates clockwise about the origin at 1 radian per time unit, and the line moves toward the axis at a constant rate of units per time unit, so that both lines reach the axis at the same time. The line meets the axis at an angle .

[less]

Contributed by: Roberta Grech (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The trisectrix can be used to trisect an angle. If a vertical line is dropped from to meet the axis at , the point on the line 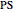is such that , and the horizontal line 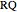meets the trisectrix at , then the angle that makes with the axis is .

Reference

[1] T. Heard, D. Martin, and B. Murphy, A2 Further Pure Mathematics, 3rd ed., London: Hodder Education 2005 p. 202, question no. 2.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send