Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Kappa Curve as a Locus

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

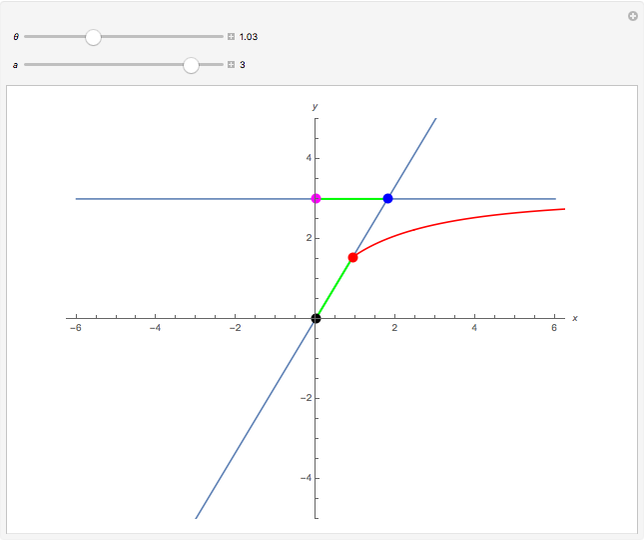
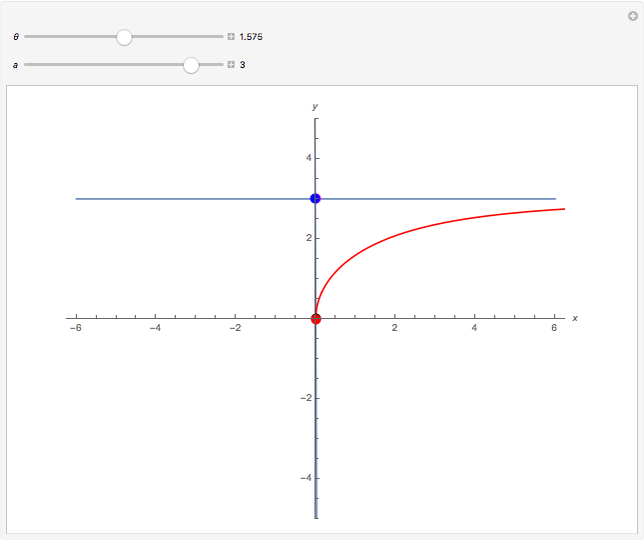
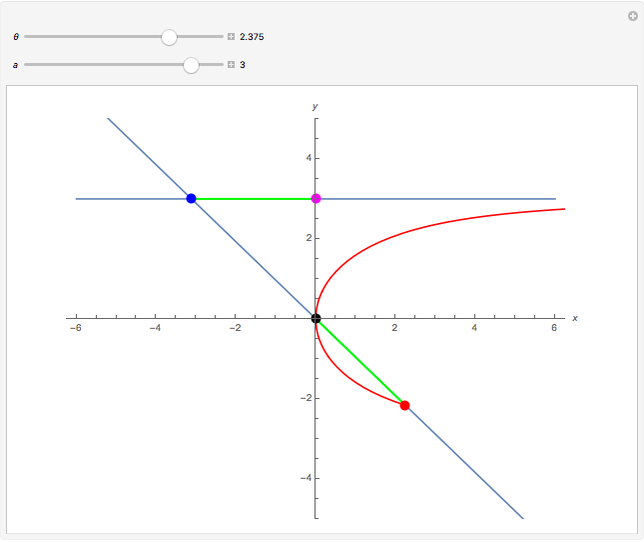
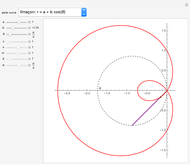
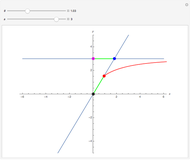
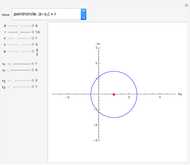
The kappa curve looks vaguely like a curly kappa, , and was studied by Newton, Bernoulli, and Gutschoven. Sometimes called Gutschoven's curve, its double cusp form can be represented as .

[more]

Let be the point (magenta). Let be the intersection point (blue) of the horizontal line with a line rotating about the origin . The kappa curve is the locus of points (red) on the rotating line such that distances (green segments).

[less]

Contributed by: Roberta Grech (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] T. Heard, D. Martin, and B. Murphy, A2 Further Pure Mathematics, 3rd ed., London: Hodder Education, 2005 p. 209, question 13.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send