Akaike Criterion in Orbit Determination

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
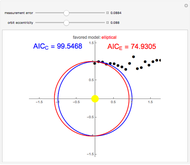
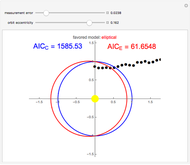
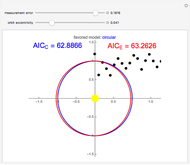
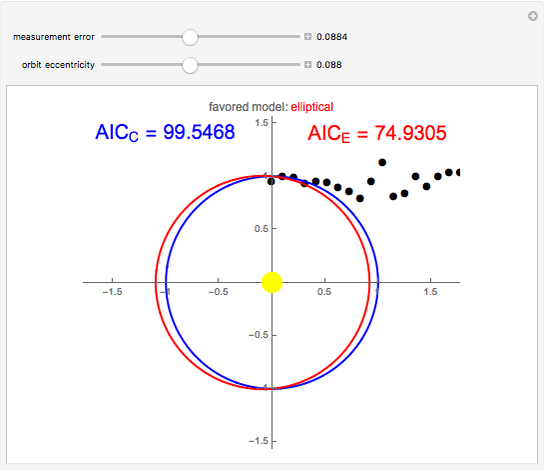
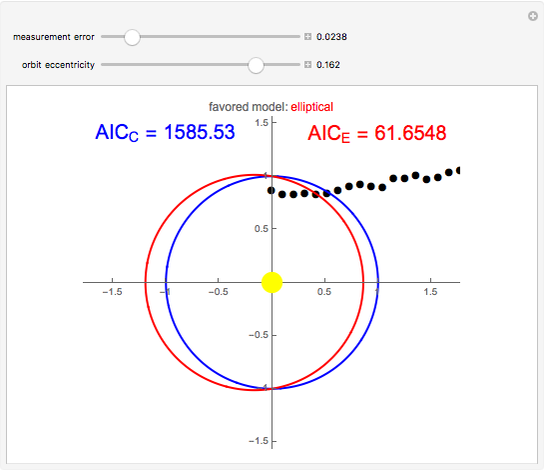
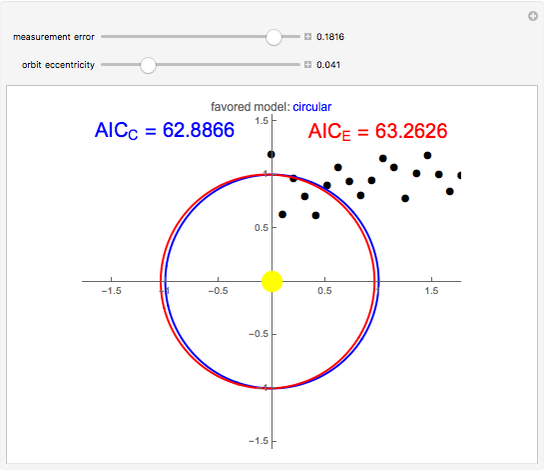
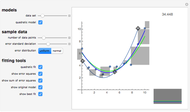
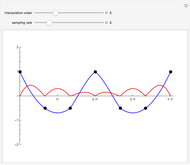
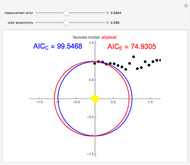
Elliptic and circular orbits are found for points lying on an ellipse perturbed by Gaussian errors. The Akaike information criterion is then used to judge which of the models is more complex. The controls allow you to change the magnitude of the errors and the shape of the unperturbed curve.
Contributed by: Tomasz Stachowiak (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration, based on the paper Kepler versus Akaike, uses the example of the Earth's orbit to show how the Akaike information criterion works for distinguishing between two models with different numbers of parameters. The points shown could be thought of as measurements of the planet's position relative to the Sun. The problem is that a circular orbit, predicting constant distance between the bodies, is always considered as the simpler one. However, the measurement error and the fact that the real orbit is not a circle causes the AIC to select the ellipse most of the time, even though it has more parameters.
For more information, see the Wikipedia entry for Akaike information criterion.
Permanent Citation
"Akaike Criterion in Orbit Determination"
http://demonstrations.wolfram.com/AkaikeCriterionInOrbitDetermination/
Wolfram Demonstrations Project
Published: March 7 2011