Alternating Planar Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
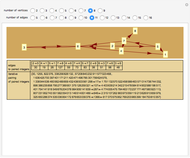
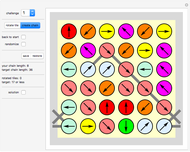
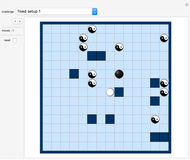
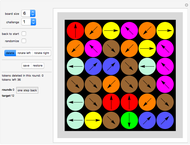
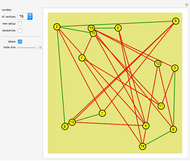
There are over 40 problems and solutions presented here relating to alternating planar graphs (where roads connect towns). You can create and redesign these graphs as you wish.
[more]
Contributed by: Karl Scherer (April 2011)
Additional contributions by: Frank Schneider, Katrin Nimczick, Lisa Schreiber, Gunnar Brinkmann
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
The term "alternating planar graph" was coined by Professor Althoefer at the University of Jena, Germany, in 1998.
In a very similar context, the term "alternating" was introduced for polygonal tilings of the Euclidean plane by Karl Scherer in his book New Mosaics (1994, privately published), which Althoefer had read. There the term was used as the condition that adjacent tiles always belong to different tile sets; these sets are characterized by the number of vertices of their prototiles (or other properties such as color).
A graph is a network of vertices and lines (straight or curved) connecting these vertices.
Practical examples are maps of towns connected by roads. Roads can only meet at towns.
In a planar graph the lines do not cross.
The degree of a vertex is the number of lines connecting to it.
"Vertex alternating" means that the degrees of any two neighboring vertices differ.
The degree of a face is the number of lines/polylines/curves (or vertices) surrounding it.
Note that the outside area also counts as a face.
"Face alternating" means that the degree of any two adjacent faces is not the same.
A planar graph is called alternating if it is a vertex-alternating and face-alternating graph.
The system does not check whether a graph is alternating. While the verification has to be done visually, the color coding of the numbers helps.
However, the degrees of vertices (all at the same time) and faces (one at a time) are calculated by the system (use actions "v degrees" and "count v", see below).
Dual graphs
Each planar graph has a dual. To obtain the associated dual graph of a given graph you reverse the roles of towns and areas (vertices and faces).
The Demonstration controls are described in the following discussion.
"challenge" control
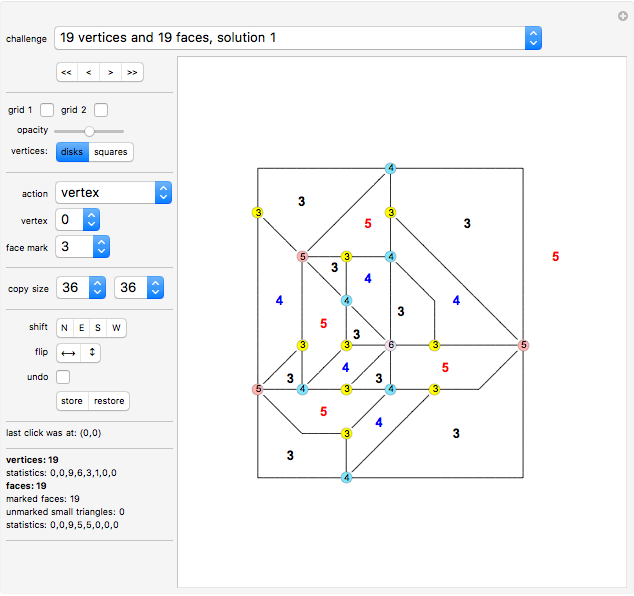
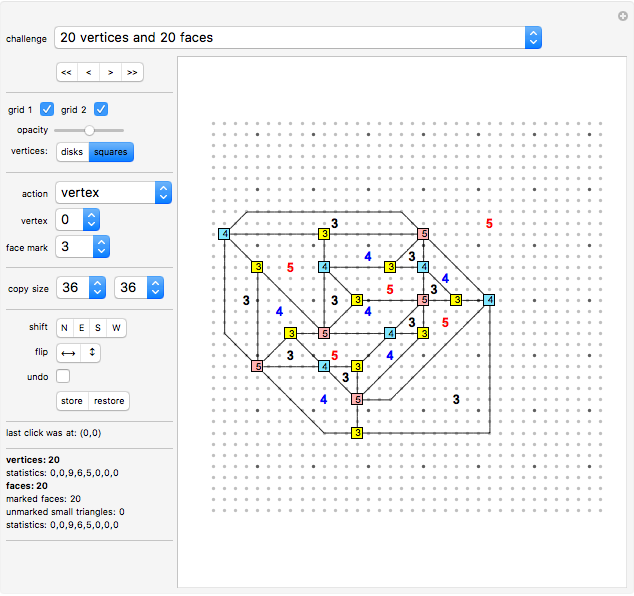
Each challenge displays a solution to a mathematical problem involving an alternating planar graph (see the following list for details).
You are invited to find other solution graphs or ones using fewer vertices or ones with a new number combination of vertices and faces.
The "Free Play" challenge shows a part of an alternating planar graph. Try to complete it!
Can you find some of them without looking at the solution?
It is easy to see that for any 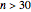 there is an alternating planar graph with
there is an alternating planar graph with  vertices:
simply join copies of the 17-vertex graph, the 21-vertex graph or the 22-vertex graph onto larger graphs.
vertices:
simply join copies of the 17-vertex graph, the 21-vertex graph or the 22-vertex graph onto larger graphs.
"<<", "<", ">", ">>" setter bar
This lets you jump to the first, previous, next, or last challenge.
"grid 1"
This button displays a grid with unit spacing.
"grid 2"
This button displays a grid with 5-unit spacing. This grid is very useful when you start designing your graph, but can be annoying later; therefore you can switch it off separately.
"opacity"
This slider controls the opacity of the background grid.
"vertices: disks/squares" setter bar
Determines whether vertices are displayed as small disks or small squares.
action "click"
This lets you click a board position to show its coordinates, even when the position is not empty.
The coordinates (in grid units) are displayed on the left border.
action "vertex"
Click a board position to drop a square representing a vertex of the graph.
You can select a numbered vertex from the "vertex" drop-down menu.
Vertices can carry numbers that represent how many lines connect to them. This number is called the "degree" of the vertex.
Vertices must be placed at least two units apart.
action "mark face"
Click a board position that is not occupied by a vertex or line segment.
A number (selected using the "face mark" drop-down menu) will be dropped on the board representing the number of vertices surrounding the area you clicked.
The system does not automatically check this number for correctness.
(However, see action "count v" that counts vertices for a clicked area.)
action "line"
Click the starting position. A red square will appear. Pink points mark where you can click next. You can always go into one of the eight main directions. Now click the target position to finish the line. The line will end in a green square.
action "polyline"
Click a starting position to start a polyline. A red square will appear. Pink points mark where you can click next. You can always go into one of the eight main directions, but you cannot go back. Click several positions that define the desired polyline. When you are done, click the last clicked position again to finish the polyline.
You cannot turn back in the next move.
Do not place vertices next to each other.
action "v chain"
This action is similar to the action "polyline", with the difference that every click creates a vertex that is connected by a straight line to the previously created vertex, resulting in a "vertex chain".
action "v degrees"
This causes the system to calculate the degrees of all vertices. In other words, for each vertex the number of lines connecting to this vertex will be calculated and (if it is greater than zero) displayed in a colored square.
Different degrees use different colors.
This is most useful when you want to check whether your graph is a vertex-alternating graph.
action "count v"
Whereas the degree of all vertices of a given graph can be calculated at one time by clicking the action "v degrees", for the degrees of the faces you have to click each area separately to let the system do the calculation.
Click an empty board position or a position that has an area marker already. The system will calculate the number of surrounding vertices for the clicked area and display it at the clicked position.
For "count v" to work, at least two lines must meet at each vertex. Furthermore, the graph must be connected.
The resulting count will be shown at the clicked position.
If you click anywhere outside the area of your graph, this action will still provide the correct result.
If you have two disconnected graphs, you still can use "count v"; just make sure that you click the board just below the partial graph you want to apply it to.
action "delete"
Click a position to erase its content.
action "del line"
Click a position to erase its content. If you clicked a line, then the whole extent of the line or polyline containing it will be erased.
action "del faces"
This will delete all face markings (this is useful during editing).
action "del horizontal"
Click the board. All entries in the same row as the clicked position will be deleted.
action "del vertical"
Click the board. All entries in the same column as the clicked position will be deleted.
action "copy"
Click the board. The part of the graph to be copied will be highlighted. It is the rectangular area with its lower-left corner in the clicked position. The size of the rectangle is determined by the "copy size" controls. You can repeatedly click the board and change the size of the copy. Once you are satisfied with your choice, select action "paste".
action "paste"
Click the board at the position where you want to place the stored part of your graph (see action "copy"). You can click the board in various places to create more copies.
action "reset"
This re-creates the default setup.
action "clear"
This clears the board.
"vertex" drop-down menu
Select the degree of the vertex that you want to paint on the board.
Then select the action "vertex" and click the board to paint this vertex onto the board.
"face mark" drop-down menu
Select the degree of the area that you want to paint on the board.
Then select the action "face mark" and click the board to paint this face onto the board.
"copy size" controls
Here you select the horizontal and vertical extent of the rectangular area of your graph that is to be copied.
These  and
and  values will be recognized by the system only when the action "copy" is active and you have clicked the board.
values will be recognized by the system only when the action "copy" is active and you have clicked the board.
"shift" controls
Click "N" to shift the whole graph one unit up; similar click "E", "S", or "W" to move the whole graph one unit right, down, or left, respectively.
"flip" controls
Click  to flip the graph horizontally or
to flip the graph horizontally or 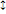 to flip the graph vertically.
to flip the graph vertically.
(You can also flip parts of a graph: you first copy and paste part of your graph to a different challenge, flip the part, then copy and paste the flipped part to your original graph.)
"undo"
Click "undo" to undo your last editing step.
It is not recommended to use "undo" in the middle of creating a polyline or a vertex chain.
If you undo a step during the creation of either a polyline or a vertex chain, then the position of the previous move will be turned into a green vertex.
"store"/"restore"
Click "store" to save the graph; click "restore" to restore it.
It is not recommended to use "store" in the middle of creating a polyline or a vertex chain.
If you store a graph during the creation of either a polyline or a vertex chain, then the position of the previous move will be turned into a green vertex when you restore the graph.
last click was at
This shows the coordinates (in grid units) of the last clicked board position.
vertices
This counter shows how many vertices are in the graph.
(vertices) statistics
This lists how many vertices are of degree 1, 2, 3, 4, 5, 6, 7, and 8, which gives a sort of "fingerprint" of a planar graph.
The statistics of the degrees of vertices and faces help you decide whether two graphs are the same or duals of each other.
Note that (green) vertices that do not display a number are only counted in the total, but not in the statistics.
faces
This counter shows the sum of "marked faces" (see below) and "unmarked small triangles" (also see below).
For alternating planar graphs, one usually requires that all faces are of degree 3 or higher.
marked faces
This counter shows how many faces have been given markers indicating the degree of a face (the number of vertices around a face).
unmarked small triangles
Small triangles (defined by a short diagonal, a vertical and a horizontal line) do not have internal space enough to carry a number (degree). Hence the system counts them separately. Note that the first versions of this Demonstration did not have this counter; hence the small triangles were missing from the face count.
(faces) statistics
This lists how many faces are of degree 1, 2, 3, 4, 5, 6, 7, and 8, which gives a sort of "fingerprint" of a planar graph.
Limitations
Only eight or fewer lines can connect to a vertex in this Demonstration.
The "count v" action only works correctly if all vertices are of degree 3 or higher, that is, if at least three lines meet at each vertex.
Do not place vertices next to each other because it will not be clear whether they are meant to be joined or not.
The system does not calculate whether your graph is indeed a vertex-alternating or face-alternating graph.
History
The current recordholder for an alternating planar graph with the fewest vertices was found on Feb 6, 2008 by Frank Schneider (University of Aachen, Germany) with the help of a computer program using beam search for planar graphs. It has 17 vertices and 17 faces.
An asymmetric alternating planar graph with 25 vertices and 25 faces is the first alternating planar graph ever found. It was found on Feb 2, 2008 by Katrin Nimczick and Lisa Schreiber (University of Jena, Germany) using only pencil and paper.
All other results given here are by Frank Schneider, Gunnar Brinkmann, and the author of this Demonstration.
The results given here have been published before as the Zillions game "Graph Puzzles" by the same author.
A very similar subject relating to planar graphs is covered by the Zillions game "Roadmaps" also by the same author.
In some alternating planar graphs, vertices and faces have degrees of only 3, 4, or 5. Jan Kristian Haugland found that in each alternating planar graph with that restriction, the number of vertices and the number of faces are equal!
Permanent Citation