Expected Returns of the Dow Industrials, Beta Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
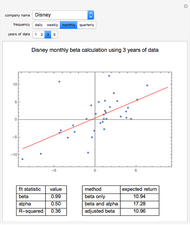
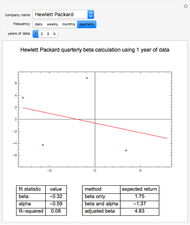
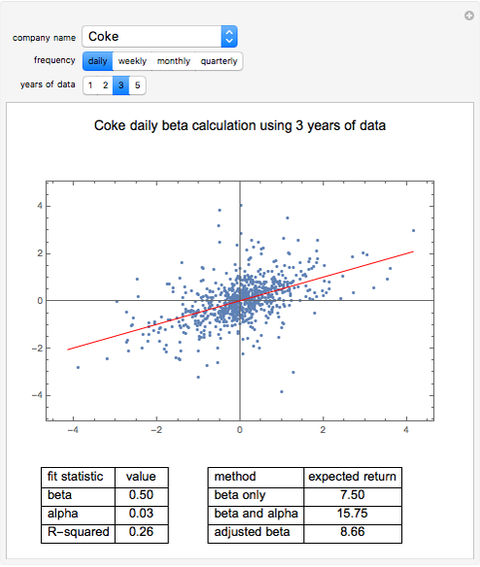
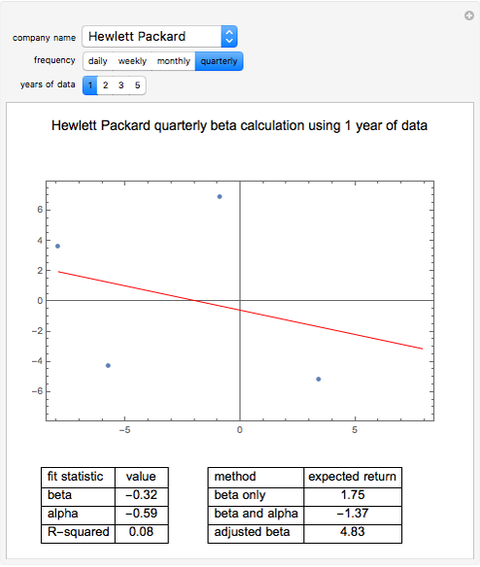
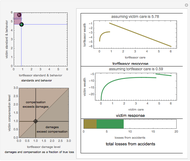
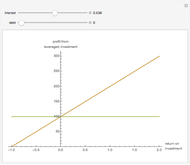
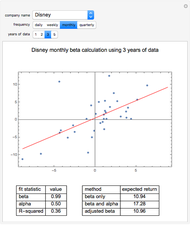
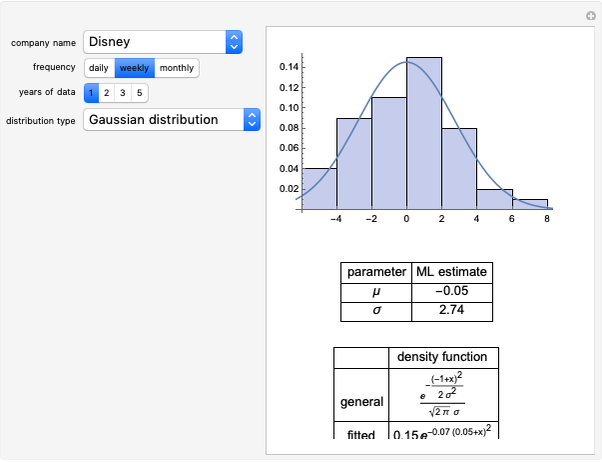
In this Demonstration, we model the expected annual returns of the components of the Dow Jones 30 using the capital asset pricing model (CAPM). We proxy the market returns using the S&P 500 (with dividends reinvested). For the specified return frequency, we display the S&P 500 returns on the  axis and the stock's returns on the
axis and the stock's returns on the 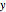 axis and show the best linear fit. The slope of this line is the beta coefficient, and the
axis and show the best linear fit. The slope of this line is the beta coefficient, and the 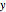 intercept is the stock's alpha (with respect to the return frequency).
intercept is the stock's alpha (with respect to the return frequency).
Contributed by: Jeff Hamrick and Jason Cawley (August 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
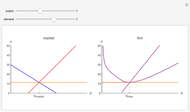
We compute three possible expected returns and display the results in the lower right-hand portion. The expected return computed with beta coefficient only is computed
according to the rule  , where
, where  is the risk-free rate,
is the risk-free rate, 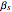 is the sample beta coefficient of stock
is the sample beta coefficient of stock  with respect to the market, and
with respect to the market, and 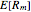 is the expected future annual return of the market. We assume that the expected future return in the market will be 11%, which has been the long-term average return of the S&P 500. We use a risk-free rate of 4%.
is the expected future annual return of the market. We assume that the expected future return in the market will be 11%, which has been the long-term average return of the S&P 500. We use a risk-free rate of 4%.
To compute the expected return "believing both beta and alpha", we use the rule 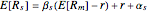 , where in this case
, where in this case 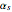 is the annualized alpha of the stock
is the annualized alpha of the stock  . In our analytical framework, a positive
. In our analytical framework, a positive  is generally obtained if the stock outperformed the market over the chosen time period. It is negative if the stock underperformed the market during the chosen time period. If the user partially believes the stock's recent alpha, the user could linearly interpolate the "beta only" and "beta and alpha" results to obtain a partial alpha of sorts.
is generally obtained if the stock outperformed the market over the chosen time period. It is negative if the stock underperformed the market during the chosen time period. If the user partially believes the stock's recent alpha, the user could linearly interpolate the "beta only" and "beta and alpha" results to obtain a partial alpha of sorts.
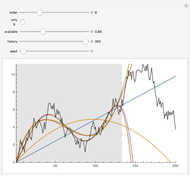
Sample beta coefficients are notorious for being unstable with respect to: (a) the return frequency used in the analysis; and (b) the particular time window of data used in the analysis. This Demonstration illustrates that instability fairly clearly. Because of this instability, some financial analysts argue that future beta coefficients should be expected to regress to the mean beta coefficient (the beta coefficient of the market with respect to itself, which is one). They instead use an adjusted beta coefficient in their analysis, determined by 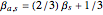 , where
, where 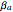 is the adjusted beta coefficient of stock
is the adjusted beta coefficient of stock  and again,
and again, 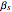 is the unadjusted beta coefficient of stock
is the unadjusted beta coefficient of stock  . We then compute another possible expected return according to the rule
. We then compute another possible expected return according to the rule 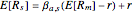 .
.
Permanent Citation