Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

An Unfoldable Polyhedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

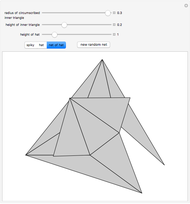
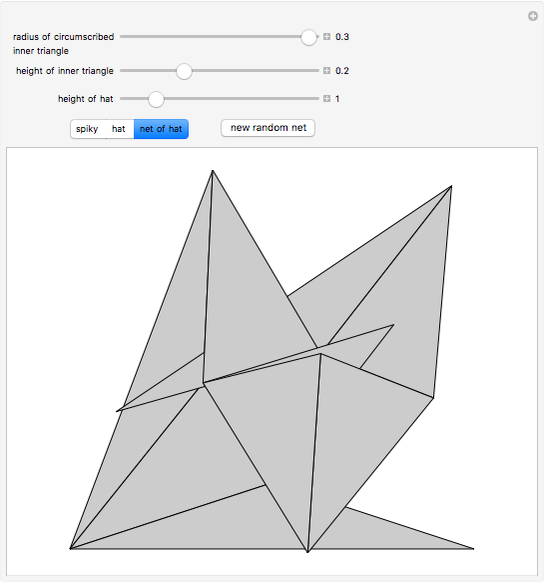
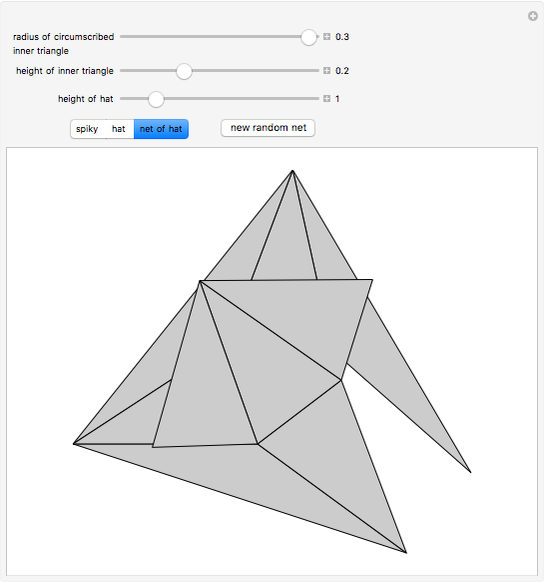
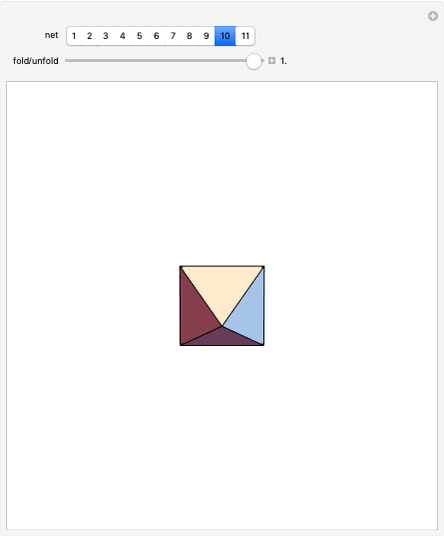
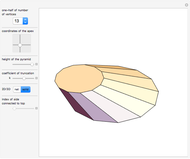
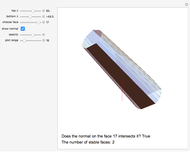
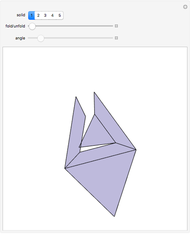
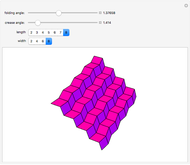
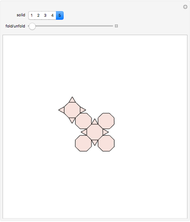
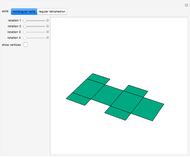
To unfold a polyhedron, cut it along some edges and flatten it out to form a net. (Allowing cuts on faces as well as edges is called a general unfolding.)

[more]

This Demonstration shows a "spiked tetrahedron" of Bern et al. [1]. It can only be unfolded with overlaps since one quarter of it (a "hat") can be unfolded only with overlaps.

[less]

Contributed by: Izidor Hafner (August 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

In [2] a polyhedron that can be edge-unfolded only with overlaps, is called an unfoldable polyhedron. The proof of the unfoldability of the spiked tetrahedron can be found in [2].

References

[1] M. Bern, E. D. Demaine, D. Eppstein and E. Kuo, "Ununfoldable Polyhedra," in Proceedings of the 11th Canadian Conference on Computational Geometry (CCCG'99), Vancouver, 1999 pp. 13-16. www.cccg.ca/proceedings/1999/fp38.pdf.

[2] E. D. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, New York: Cambridge University Press, 2007, pp. 318–320.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send