Four Polyhedra, Each with an Unfolding that Overlaps Itself

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
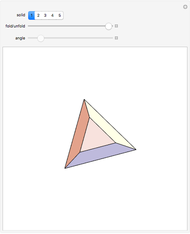
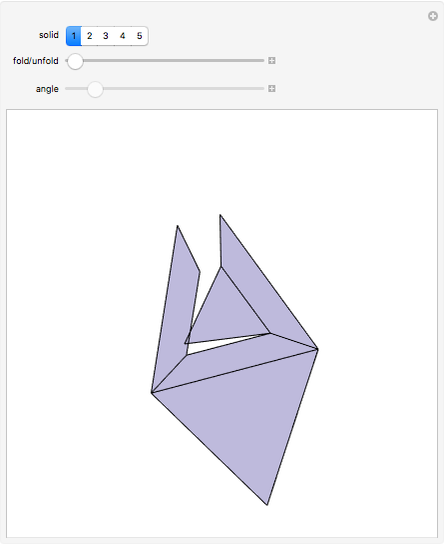
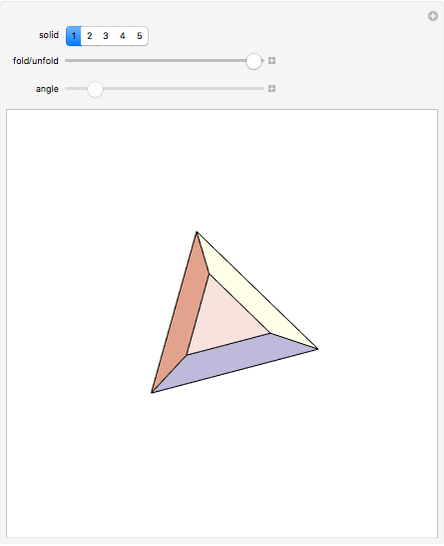
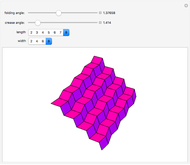
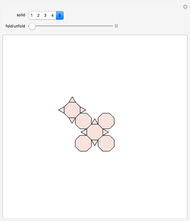
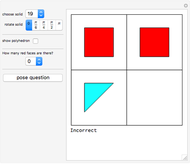
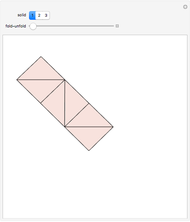
This Demonstration originally showed four polyhedra, each with a self-overlapping unfolding. A fifth has been added.
Contributed by: Izidor Hafner (June 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
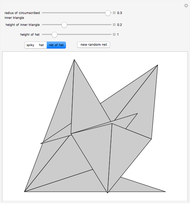
The fifth case is an axample of a volcano unfolding. A volcano unfolding of a prismoid cuts every side edge, does not cut any bottom edge, and the top is attached to the top of one flap (side face). A theorem states that a prismoid has a volcano unfolding that does not overlap [1, p. 321]. An example of a prismoid of decagon base with volcano unfolding that overlaps is given [1, p. 323]. The term "volcano" makes sense if a prismoid in form of truncated  -gonal pyramid with large
-gonal pyramid with large  is considered.
is considered.
A net of a polyhedron is an example of a tree. In case of volcano unfolding the net is constructed using breadth-first traversal, while the other examples don't use it.
[1] E. D. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, New York: Cambridge University Press, 2007.
Permanent Citation
"Four Polyhedra, Each with an Unfolding that Overlaps Itself"
http://demonstrations.wolfram.com/FourPolyhedraEachWithAnUnfoldingThatOverlapsItself/
Wolfram Demonstrations Project
Published: June 6 2008