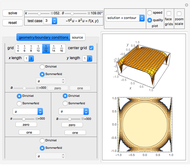
Analysis of a Single-Span Euler-Bernoulli Beam under Different Loading Conditions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
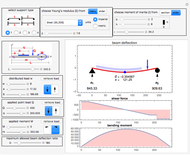
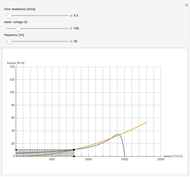
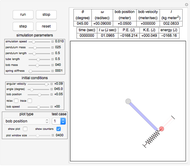
This Demonstration shows a single-span Euler–Bernoulli beam under four possible support conditions and with three different loading arrangements.
[more]
Contributed by: Nasser M. Abbasi (March 2011)
Open content licensed under CC BY-NC-SA
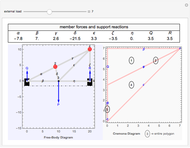
Snapshots
Details
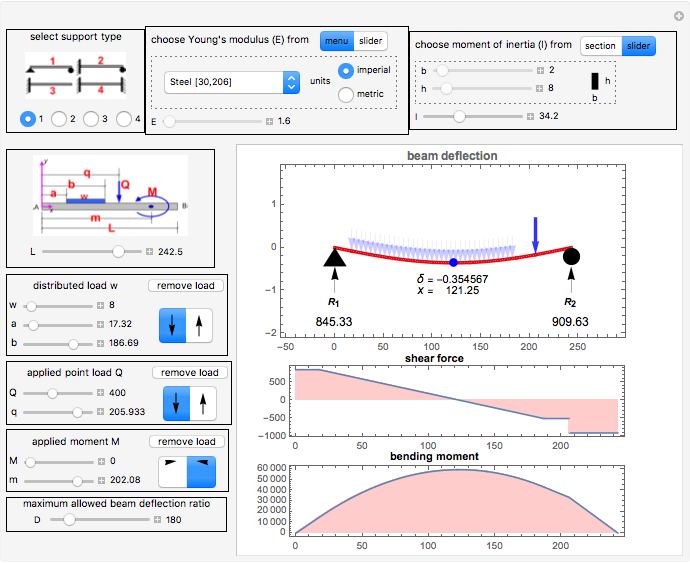
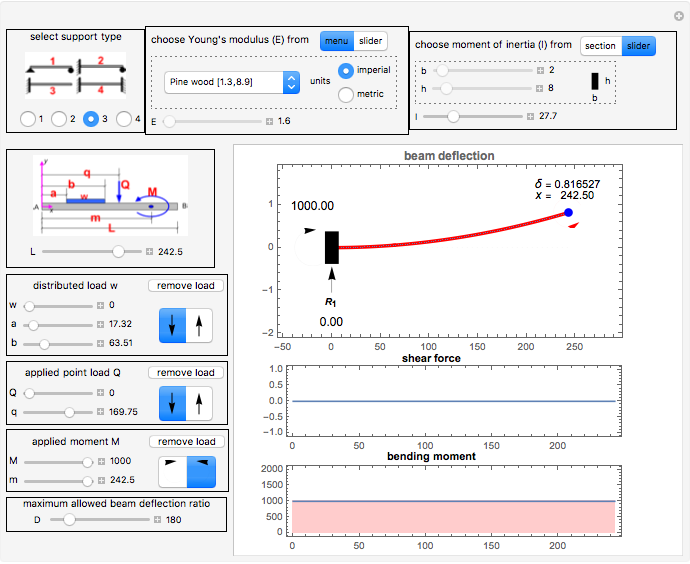
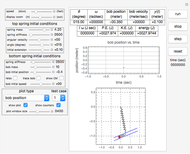
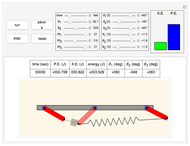
First, select one of the four different support conditions for the beam in the diagram at the top-left corner. The beam length is selected using the length slider located below this diagram.
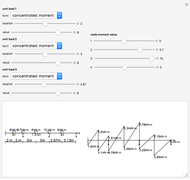
Select the loadings with the controls on the left side. A diagram is included that describes the different dimensions that define the loading positions and geometry. Using this diagram with the corresponding control variables, you can define different loading configurations.
Three different load types are supported: point load 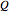 with units of force, distributed load
with units of force, distributed load 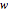 with units of force per unit length, and a couple
with units of force per unit length, and a couple 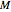 with units of force times length.
with units of force times length.
Select the Young's modulus 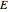 from either the slider or by directly choosing the material from the dropdown menu. The numbers shown for the values of
from either the slider or by directly choosing the material from the dropdown menu. The numbers shown for the values of 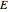 in this menu selection are the numerical values for
in this menu selection are the numerical values for 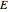 for the selected material. The first number is in imperial units (
for the selected material. The first number is in imperial units (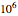 psi) and the second is in metric units (
psi) and the second is in metric units ( Pa). These values are obtained from standard materials references. When the slider for
Pa). These values are obtained from standard materials references. When the slider for 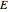 is selected, each value is multiplied by
is selected, each value is multiplied by 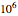 . For example, to select a material whose
. For example, to select a material whose 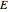 is 1,600,000 psi, set the slider to
is 1,600,000 psi, set the slider to 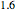 .
.
The moment of inertia 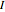 is selected using the slider or by defining the geometry of the beam cross section. Only rectangular cross section is supported. In the cross section option, the moment of inertia is calculated using the standard formula
is selected using the slider or by defining the geometry of the beam cross section. Only rectangular cross section is supported. In the cross section option, the moment of inertia is calculated using the standard formula 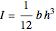 .
.
The deflection  that the beam will experience is limited to a fixed value controlled by the parameter
that the beam will experience is limited to a fixed value controlled by the parameter  labeled "deflection ratio", located at the lower-left part of the control area. A deflection ratio of
labeled "deflection ratio", located at the lower-left part of the control area. A deflection ratio of  means that the beam's maximum deflection will not be allowed to exceed
means that the beam's maximum deflection will not be allowed to exceed 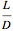 , where
, where 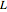 is the beam length. These ratios can be found in standard structural engineering references such as the International Building Code. Increasing the value of
is the beam length. These ratios can be found in standard structural engineering references such as the International Building Code. Increasing the value of 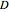 restricts the allowed maximum deflection of the beam to smaller values. For a typical beam used in housing construction,
restricts the allowed maximum deflection of the beam to smaller values. For a typical beam used in housing construction, 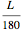 can be used.
can be used.
Once the maximum beam deflection 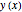 (in absolute value) has reached the numerical value
(in absolute value) has reached the numerical value 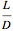 , a warning message is displayed inside the beam deflection plot indicating that the beam has failed. In this case, you can reduce the beam length, increase
, a warning message is displayed inside the beam deflection plot indicating that the beam has failed. In this case, you can reduce the beam length, increase 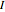 , increase
, increase 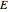 , or reduce the current loading on the beam.
, or reduce the current loading on the beam.
The plot range for the 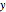 axis for the deflection curve is kept fixed at the maximum allowed deflection value in order to make it easier to see how the beam deflection changes as loads and other parameters are changed.
axis for the deflection curve is kept fixed at the maximum allowed deflection value in order to make it easier to see how the beam deflection changes as loads and other parameters are changed.
Regarding the use of units in this illustration: use numerical values for the different parameters either in metric units or imperial units. It is the user's responsibility to make sure that values being selected for the different parameters are consistent with each other. For example, with length 10 feet and moment of inertia 57 inches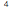 , if the moment of inertia is entered as the number 57, the length should be entered as 120 and not as 10.
, if the moment of inertia is entered as the number 57, the length should be entered as 120 and not as 10.
When selecting 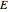 from the dropdown menu, choose either metric or imperial for the units to be consistent with the units being used for the other parameters.
from the dropdown menu, choose either metric or imperial for the units to be consistent with the units being used for the other parameters.
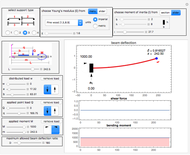
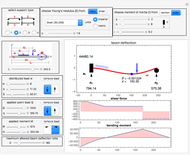
In the three plots generated, the  axis has length units and represents the beam length. For the deflection curve
axis has length units and represents the beam length. For the deflection curve  , the
, the 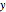 axis is the amount of deflection in units of length. For the bending moment diagram, the
axis is the amount of deflection in units of length. For the bending moment diagram, the 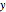 axis has units of force times length, and for the shear force diagram, the
axis has units of force times length, and for the shear force diagram, the 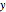 axis has units of force.
axis has units of force.
To find the deflection at any location along the beam, move the mouse to the location over the deflected beam curve.
The small blue ball on the deflection curve indicates the location of the maximum deflection. The deflection value at that point and the distance from the left end of the beam are displayed next to the ball.
Permanent Citation