Dynamics of Two Cylinders with Three Springs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
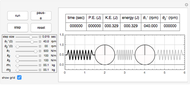
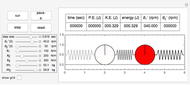
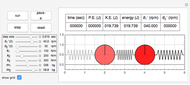
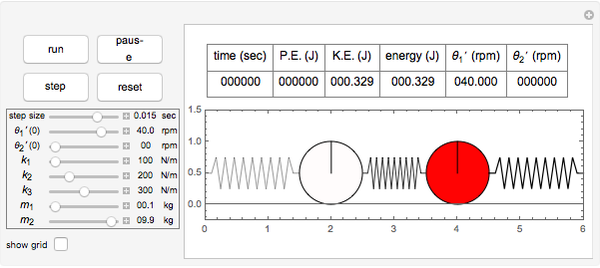
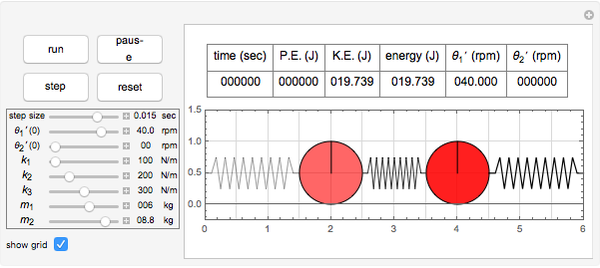
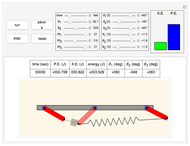
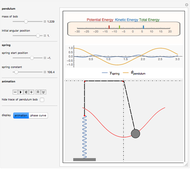
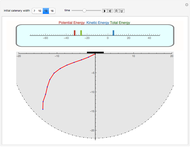
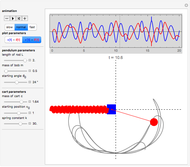
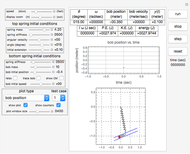
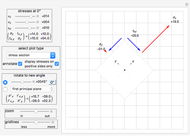
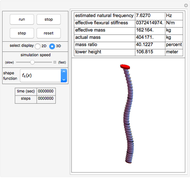
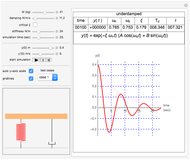
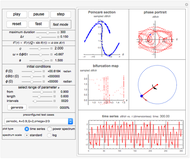
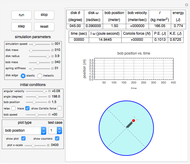
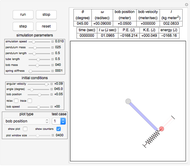
This Demonstration determines the solution of a discrete system of two cylinders connected by three springs. You can adjust the mass of each cylinder and the stiffness of each spring to see the effect on the dynamics of the system. The left and right cylinders have masses 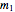 and
and 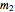 , respectively. The spring stiffness values are
, respectively. The spring stiffness values are 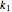 ,
, 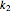 , and
, and 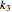 from left to right. You can adjust the initial angular velocity of either cylinder. The initial angular position is assumed to be zero. The equations of motion are derived using the Lagrangian method. The author
s report contains the mathematical derivation of the equations of motion. Cylinders roll without slipping and the system has two degrees of freedom
from left to right. You can adjust the initial angular velocity of either cylinder. The initial angular position is assumed to be zero. The equations of motion are derived using the Lagrangian method. The author
s report contains the mathematical derivation of the equations of motion. Cylinders roll without slipping and the system has two degrees of freedom 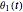 and
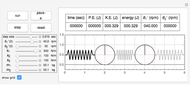
and 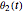 . The system potential energy, kinetic energy, and total energy are displayed in the table at the top. Since zero friction and damping are assumed, the total energy remains constant.
. The system potential energy, kinetic energy, and total energy are displayed in the table at the top. Since zero friction and damping are assumed, the total energy remains constant.
Contributed by: Nasser M. Abbasi (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Dynamics of Two Cylinders with Three Springs"
http://demonstrations.wolfram.com/DynamicsOfTwoCylindersWithThreeSprings/
Wolfram Demonstrations Project
Published: August 8 2013