Riccati Differential Equation with Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
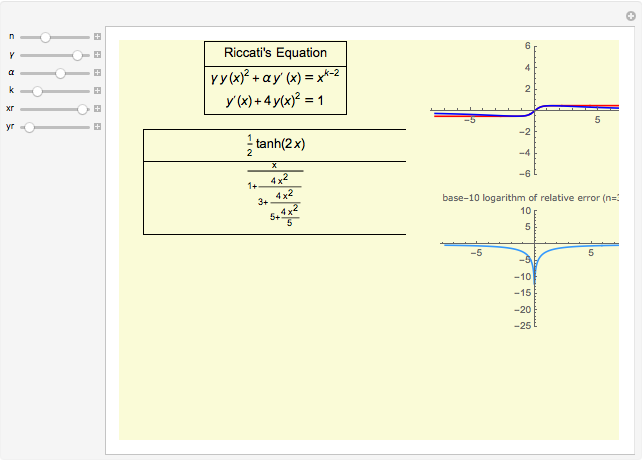
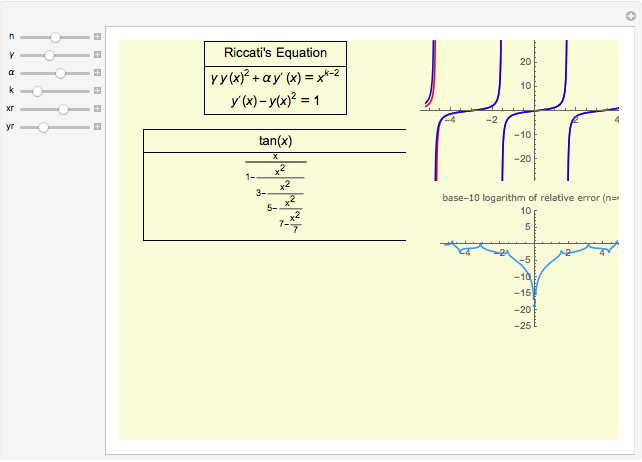
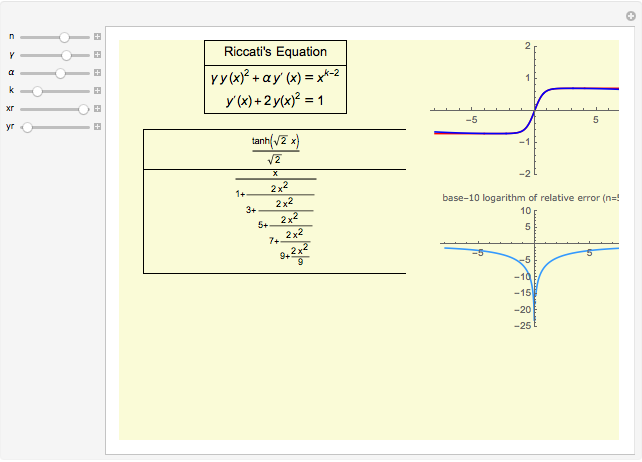
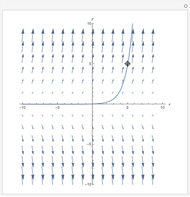
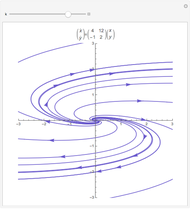
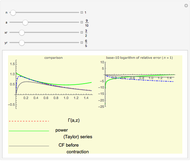
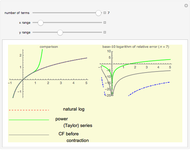
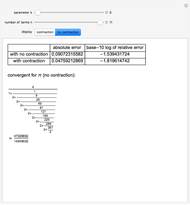
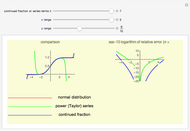
Explore the solutions of the Riccati differential equation with continued fractions, which provide a very effective function approximation toolset. Usually the continued fraction expansion of a function approximates the function better than its Taylor or Fourier series. The solution(s) of the Riccati differential equation are very diverse; they contain polynomials, trigonometric and hyperbolic functions, logarithms, and (nested) square roots.
Contributed by: Andreas Lauschke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
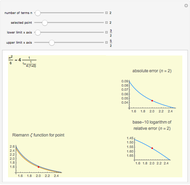
The solutions of the Riccati differential equation are ratios of Bessel functions. In many cases these simplify to monomials, combinations of trigonometric functions, and logarithms. The number of terms used in the continued fraction expansion is  ,
, 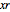 is the domain on the
is the domain on the  axis ("
axis (" range"), and
range"), and 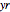 is the range of values displayed on the
is the range of values displayed on the 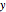 axis ("
axis ("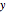 range").
range").
Permanent Citation
"Riccati Differential Equation with Continued Fractions"
http://demonstrations.wolfram.com/RiccatiDifferentialEquationWithContinuedFractions/
Wolfram Demonstrations Project
Published: March 7 2011