Balancing Abstract Chemical Equations with One Kind of Atom
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
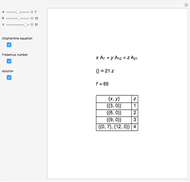
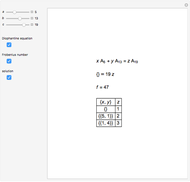
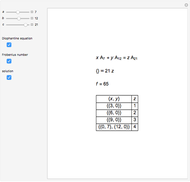
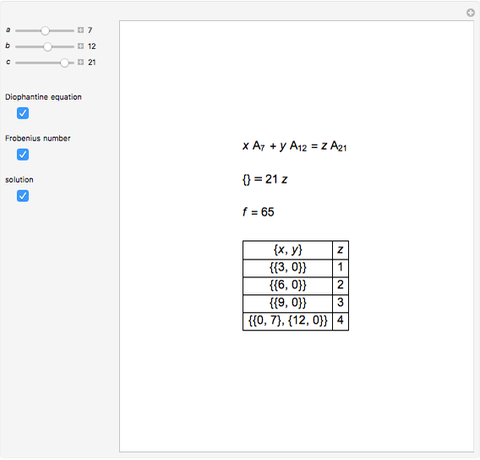
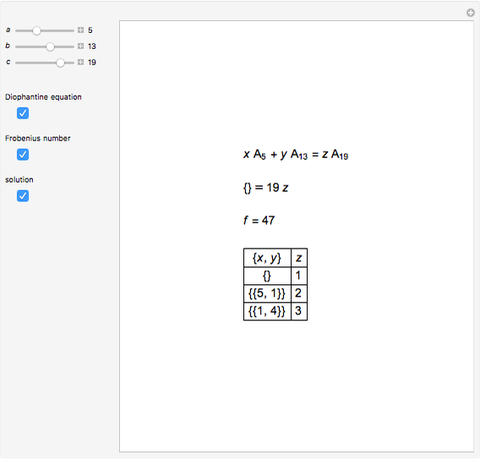
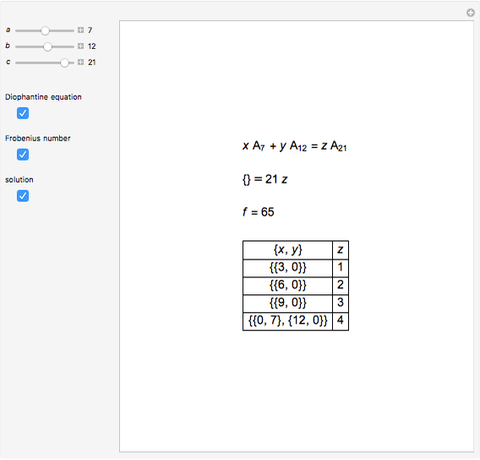
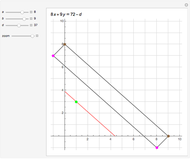
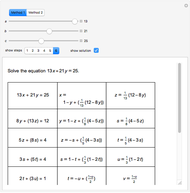
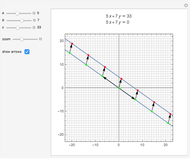
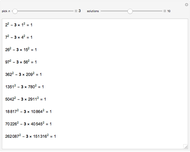
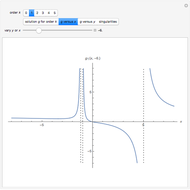
This Demonstration solves chemical-like equations with one kind of atom, represented by the letter  . An expression like
. An expression like  can be thought of as a "molecule" of
can be thought of as a "molecule" of  atoms of
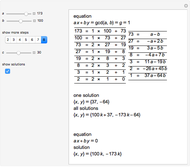
atoms of  . For the equation to be balanced, the counts of the atoms on both sides must be the same. Balancing the equation
. For the equation to be balanced, the counts of the atoms on both sides must be the same. Balancing the equation  is equivalent to solving the Diophantine equation
is equivalent to solving the Diophantine equation  , where parameters
, where parameters  ,
,  , and
, and  are positive integers, and the solution should be in non-negative integers
are positive integers, and the solution should be in non-negative integers  ,
,  and positive
and positive  .
.
Contributed by: Izidor Hafner (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation