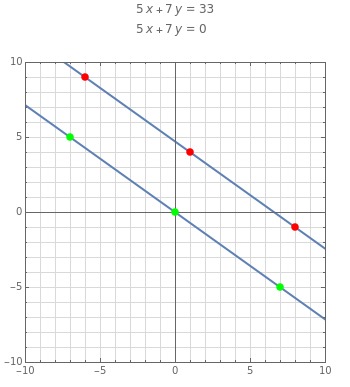
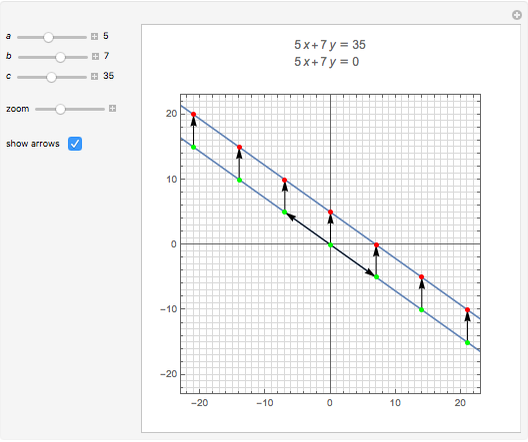
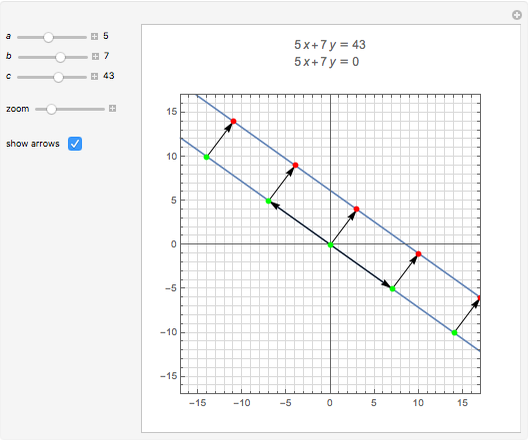
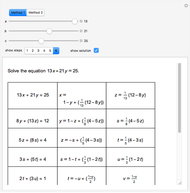
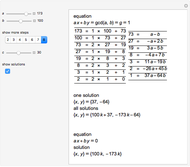
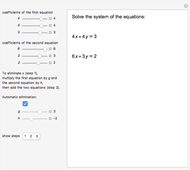
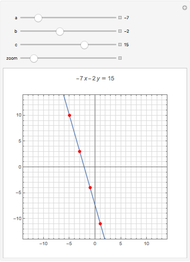
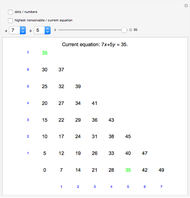
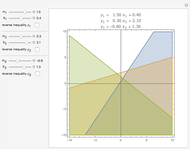
A linear Diophantine equation in two variables has the form , with , , and integers, where solutions are sought in integers. The corresponding homogeneous equation is , and it always has infinitely many solutions , where is an integer. If is a solution of the nonhomogeneous equation, all of its solutions are of the form . Suppose and are positive and relative prime. Then the distance between two consecutive solutions is , so the equation always has a solution in non-negative integers if .