Beraha's Conjecture and Cyclic Graphs
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
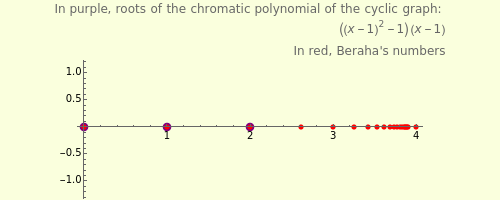
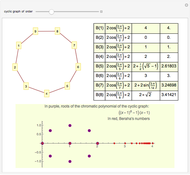
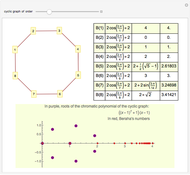
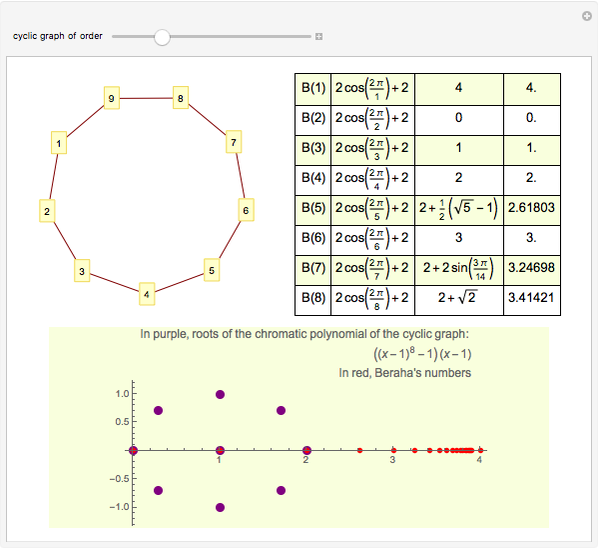
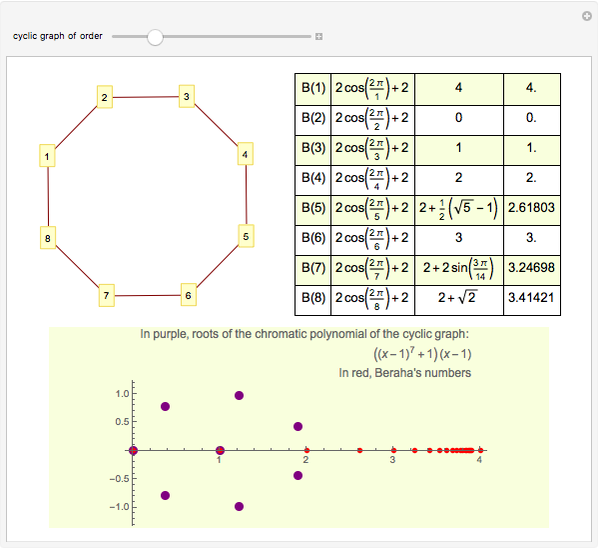
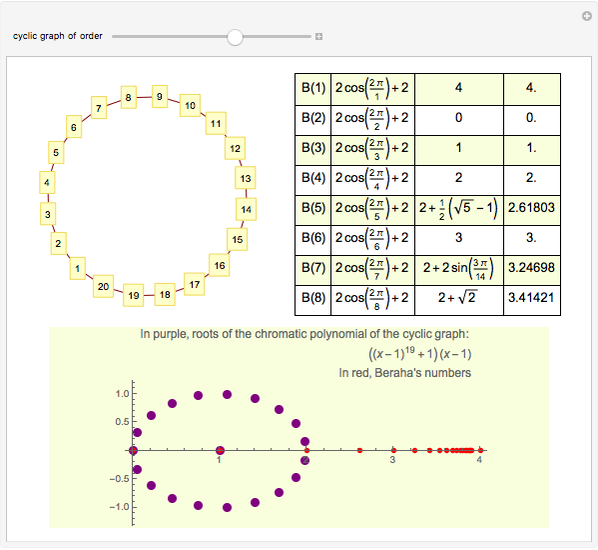
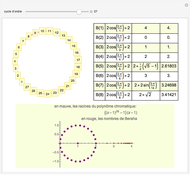
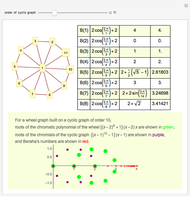
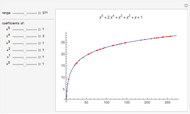
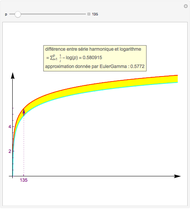
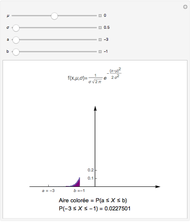
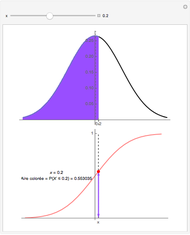
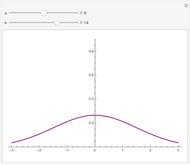
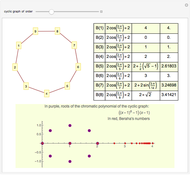
The chromatic polynomial of a graph gives the number of ways to color the graph with  colors, such that no pair of connected vertices shares the same color.
colors, such that no pair of connected vertices shares the same color.
Contributed by: Jacqueline Zizi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation