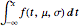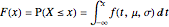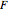Fonction de répartition (French)
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
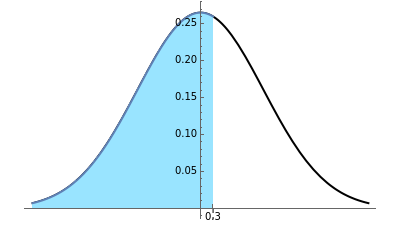
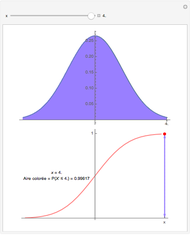
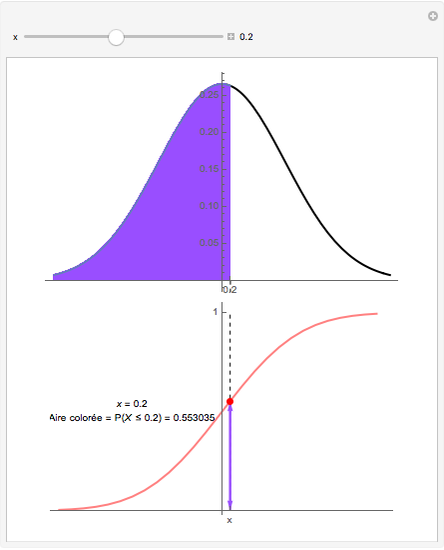
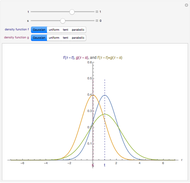
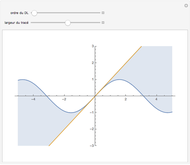
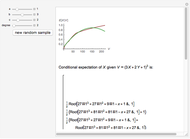
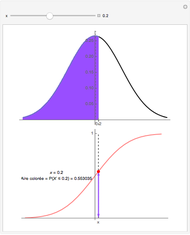
Soit 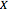 une variable aléatoire continue de densité de probabilité
une variable aléatoire continue de densité de probabilité 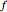 , par exemple gaussienne, comme ci-dessus. Cette densité de probabilité
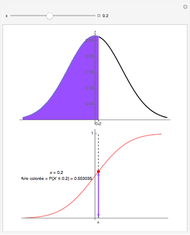
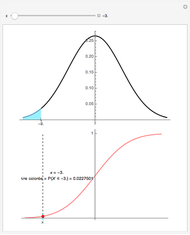
, par exemple gaussienne, comme ci-dessus. Cette densité de probabilité 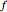 est représentée par la courbe noire sur le dessin du haut.
est représentée par la courbe noire sur le dessin du haut.
Contributed by: Jacqueline Zizi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation