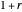Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

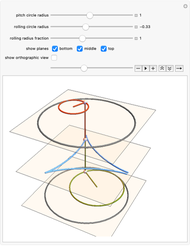
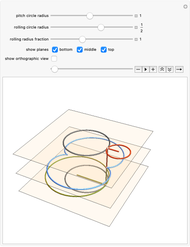
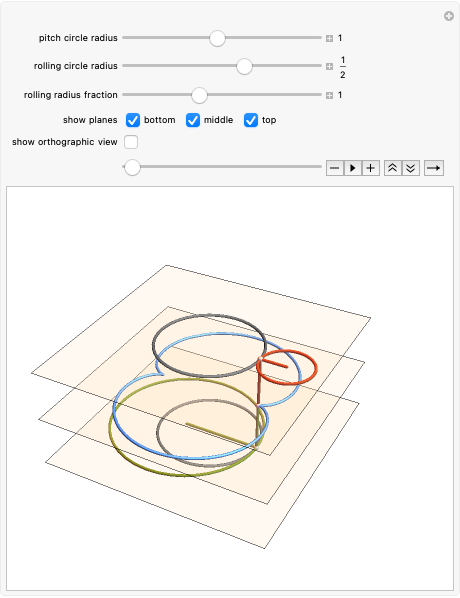
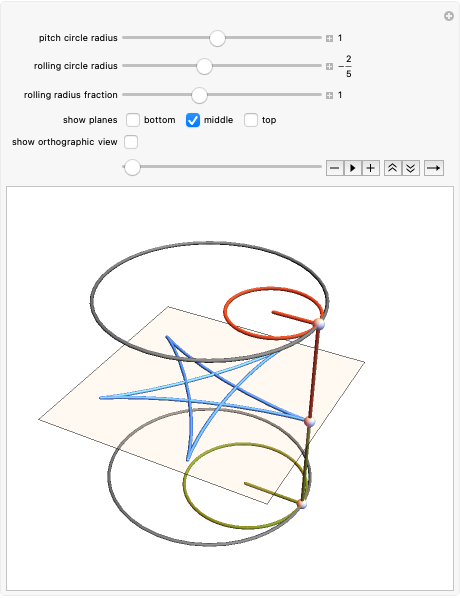
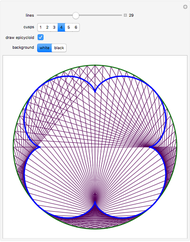
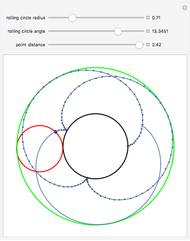
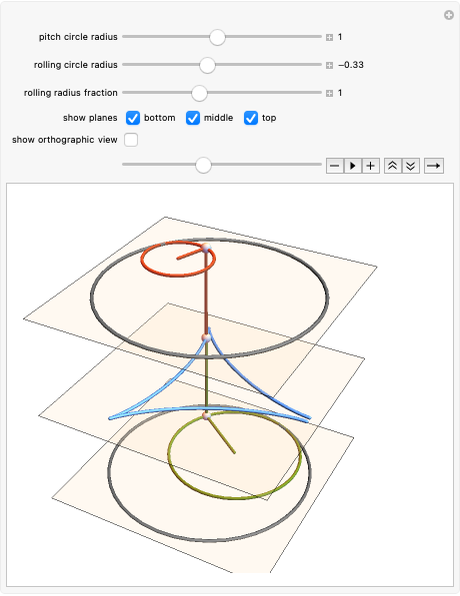
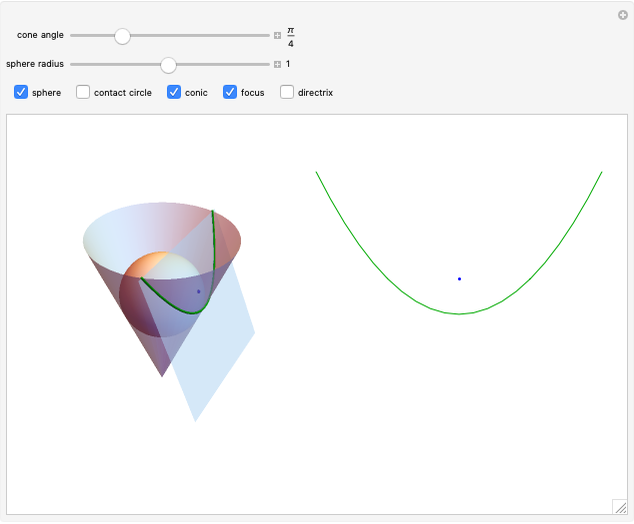
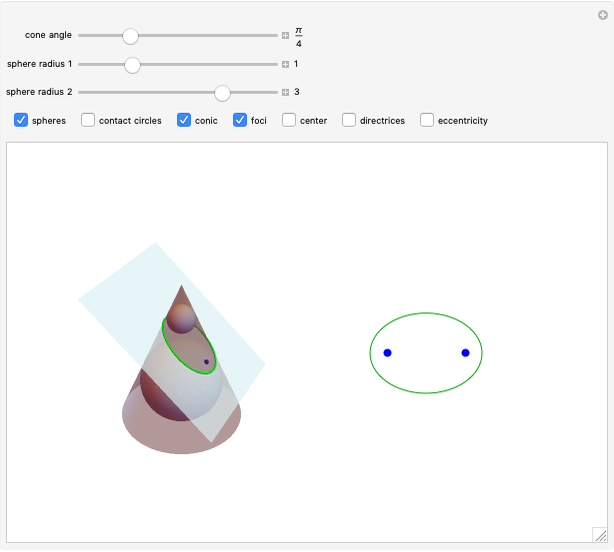
This Demonstration generates a circle roulette in 3D in two equivalent ways, in accordance with the "double generation" theorem of Euler and Bernoulli. We get a hypotrochoid or epitrochoid, depending on whether the rolling circle is inside or outside the fixed circle.

[more]

The Bernoulli–Euler double generation theorem for circle roulettes can be stated as follows. Let the pitch (or fixed) circle have radius of 1. Then:

1. An epicycloid generated by a rolling circle of radius r is equivalent to a hypocycloid (or pericycloid) with a rolling circle of radius .

2. A hypocycloid generated by a rolling circle of radius r is equivalent to a hypocycloid with a rolling circle of radius 1-r.

The theorem can be suitably generalized to epitrochoids and hypotrochoids, in which the point mounted on the rolling circle is not necessarily placed at the circle's rim.

[less]

Contributed by: Jan Mangaldan (May 8)
Open content licensed under CC BY-NC-SA

Details

References

[1] E. H. Lockwood, A Book of Curves, Cambridge, England: Cambridge University Press, 1961. https://www.cambridge.org/core/books/book-of-curves/F08B52C8FB0563B2F9866DA186FC87F1.

[2] R. C. Yates, A Handbook on Curves and Their Properties, Washington, DC: National Council of Teachers of Mathematics, 1952.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send