Salzer's Method for Numerical Evaluation of Inverse Laplace Transform Involving a Bessel Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
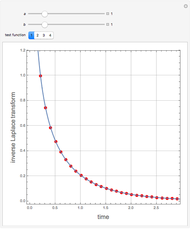
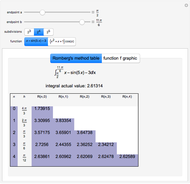
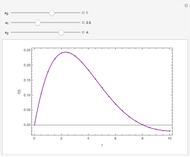
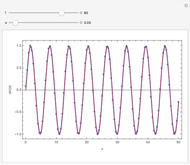
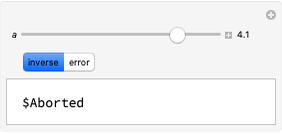
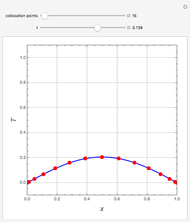
This Demonstration shows the numerical inversion of Laplace transforms using Herbert E. Salzer's method [1]. The test function is  , where the user sets the parameter
, where the user sets the parameter  . The exact inverse Laplace transform is given by
. The exact inverse Laplace transform is given by 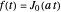 , where
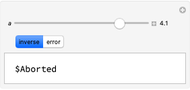
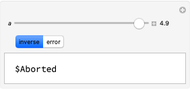
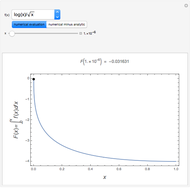
, where  is the Bessel function of the first kind of order zero. The error (i.e. the difference between the exact inverse and the numerical inverse) is also given. The numerical method fails at large
is the Bessel function of the first kind of order zero. The error (i.e. the difference between the exact inverse and the numerical inverse) is also given. The numerical method fails at large  (see the first snapshot) and can only serve as a quick-and-dirty technique for the inversion of Laplace transforms.
(see the first snapshot) and can only serve as a quick-and-dirty technique for the inversion of Laplace transforms.
Contributed by: Housam Binous (January 2014)
After work by: Jan Mangaldan
Open content licensed under CC BY-NC-SA
Snapshots
Details
Herbert E. Salzer's method allows the determination of  for a given
for a given  as follows:
as follows:
 , where
, where  are the roots of
are the roots of 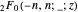 ,
,  are the Christoffel numbers, and
are the Christoffel numbers, and  are the generalized hypergeometric functions.
are the generalized hypergeometric functions.
Reference
[1] H. E. Salzer, "Orthogonal Polynomials Arising in the Numerical Evaluation of Inverse Laplace Transforms," Mathematics of Computation, 9(52), 1955 pp. 164–177. doi: 10.1090/S0025-5718-1955-0078498-1.
Permanent Citation