Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Circular Regression

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

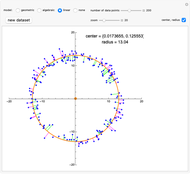
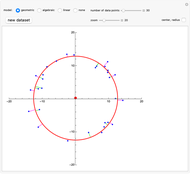
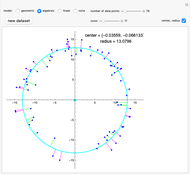
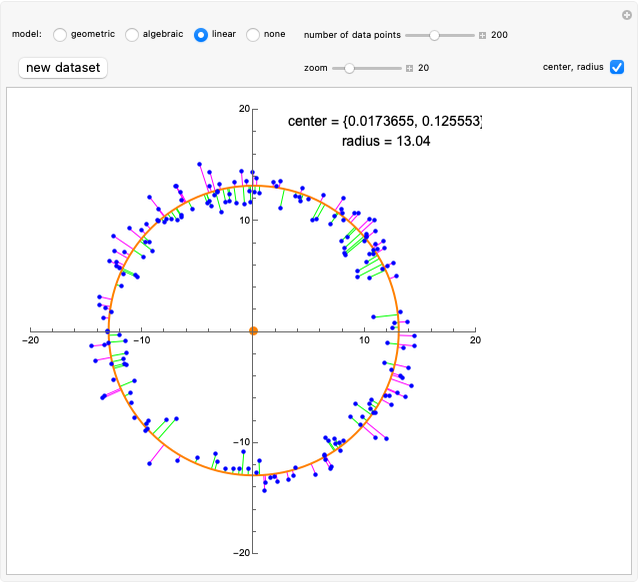
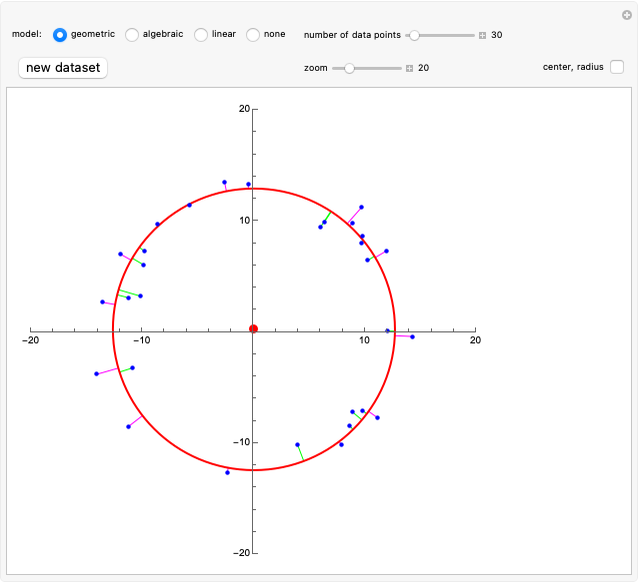
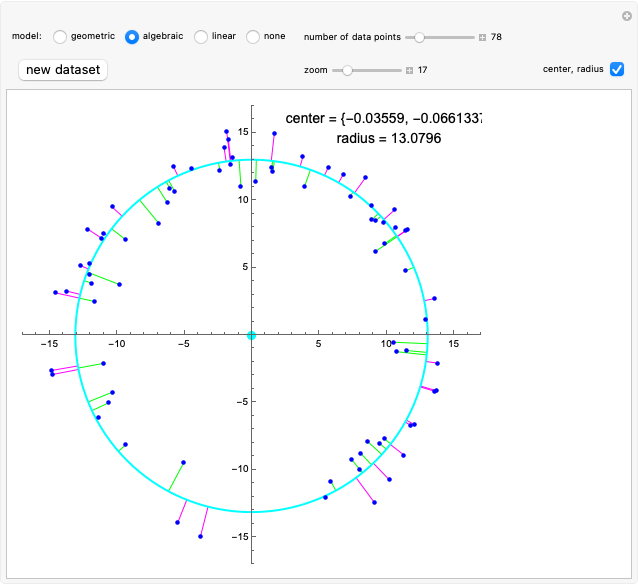
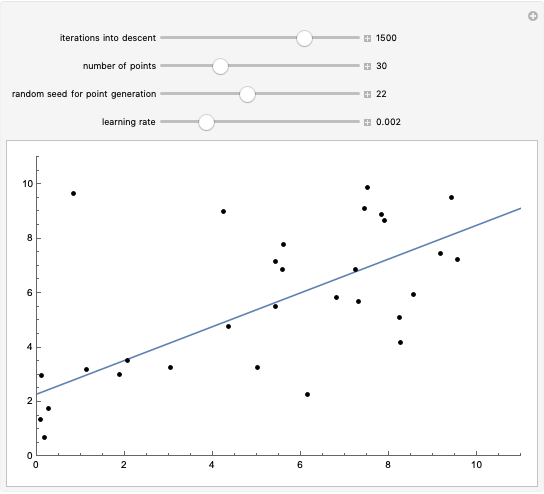
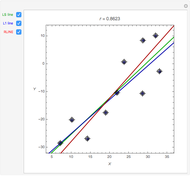
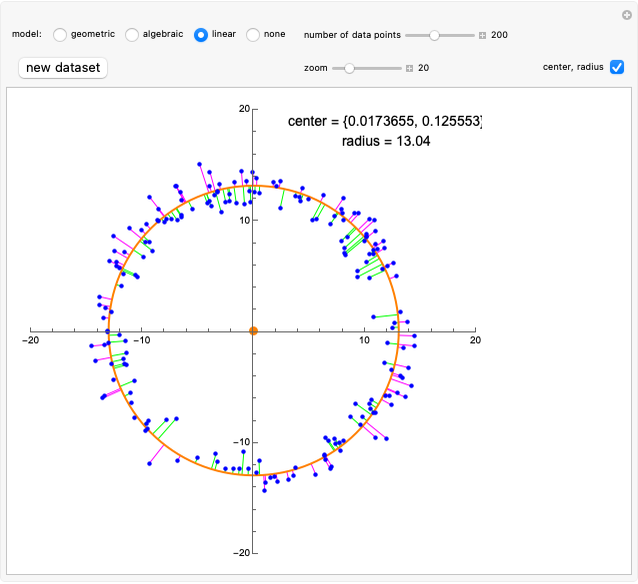
This Demonstration considers an application of circular regression. Starting with a scatter plot of experimental data, we try to determine the center and radius of the circle that best fit the observations.

[more]

The first application of least squares minimizes the objective function with center at and radius :

.

Since this represents the averaged distance of the observed points from the optimal circumference, it is referred to as a geometric fit.

The second objective function is referred to as an algebraic fit:

.

In the latter case, an expedient redefinition of the parameters reduces the problem to a linear regression.

[less]

Contributed by: Lorenzo Roi (June 13)
Open content licensed under CC BY-NC-SA

Details

Reference

[1] N. Chernov, Circular and Linear Regression: Fitting Circles and Lines by Least Squares, Boca Raton: Taylor & Francis, 2010.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send