Comparing Ambiguous Inferences when Probabilities Are Imprecise

The truth table in the upper part of the Demonstration shows the four logical possibilities for the two propositions and being true or false together. The frequency counts there are controlled by the upper set of sliders. At the arbitrary default levels, 20 out of 100 of the counts are associated with the proposition being true () (columns 1 and 2), giving a base rate for the truth of the proposition of 20 out of 100, shown as a triangle on the axis at 0.2 in the figure. The sensitivity of the diagnostic test is the conditional probability, , initially set at 16 out of 20 (from columns 1 and 2), and shown as a circle on the right-hand margin of the graph. A good diagnostic should pick up the state when it is present. The specificity of the test is another conditional probability, , which is initially set at 56 out of 80 (from columns 3 and 4), and is shown as a circle on the left-hand margin of the graph at a height of 30%, the false positive rate for the diagnostic test, . A good diagnostic should indicate the absence of the state when it is indeed absent. Applying Bayes's theorem, the resulting precise posterior probability for being true given a positive diagnostic, , is 40%, 16 out of 40 (from columns 1 and 3 in the table), shown as a large square box on the top margin of the axis. A corresponding smaller square on the axis along the bottom margin finds the level of the other posterior probability, , but in this Demonstration we are concentrating on how to interpret a positive diagnostic signal.

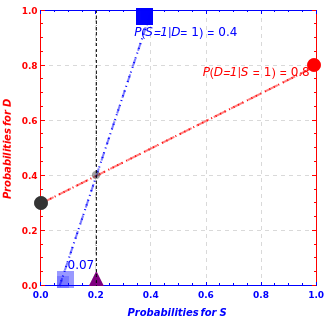
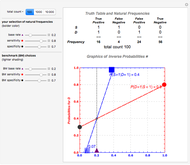
The dashed lines in the graph are coherency constraints on the inference process. The marginal probability for the diagnostic test result being positive, 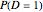, is a weighted average of the sensitivity, , and the false positive rate, , (1- specificity), as specified in the linear equation:

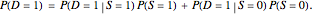
This equation is represented by the dashed red line between the two circles on the right- and left-hand margins of the graphical interface.

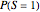is the marginal or unconditional probability of the proposition that 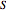is true (). It too must be an appropriate weighted average of posterior inferences about the state given various levels of the diagnostic signal, as specified in the following linear equation:

.

The blue dotted/dashed line between the two squares on the top and bottom horizontal axes expresses this linear relationship.

The intersection of the red and blue dashed lines solves for the unique pair of marginal probabilities, 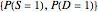, that satisfies both linear relationships.

The above two linear relationships are not logically independent. Changing any of the three components of one of the linear relationships means the components of the other relationship change as well. The Demonstration is set up so that the sensitivity, specificity, and base rate that define the red dotted/dashed line between the two circles can be changed by the sliders, and the endpoints of the corresponding changes in the blue dotted/dashed line between the two squares trace out the relevant posterior inferences, 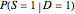and , with the emphasis on the former.

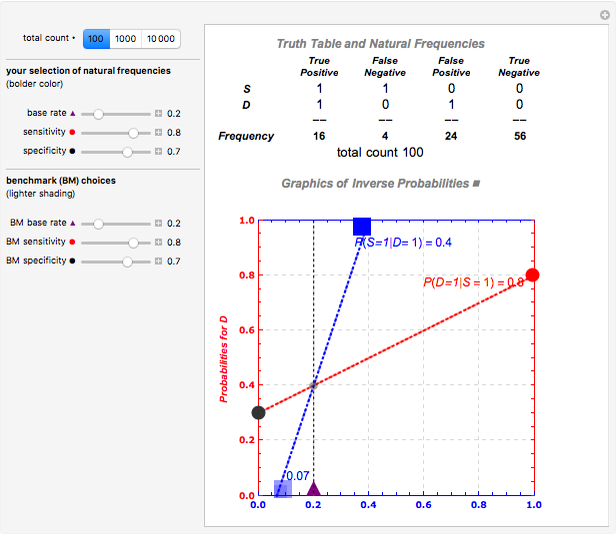
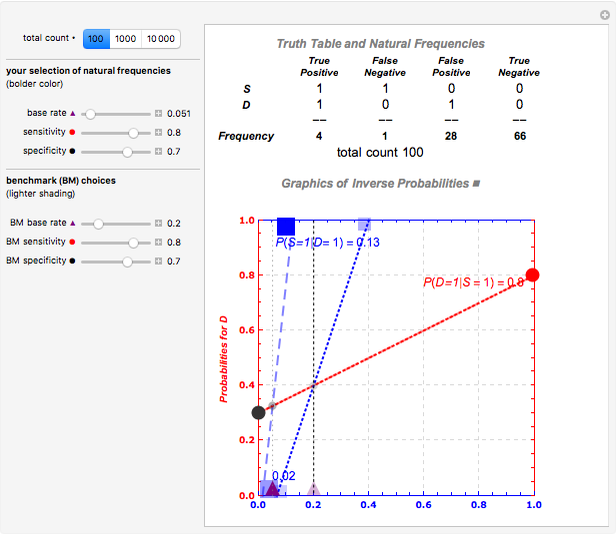
There are two sets of sliders, one for benchmark purposes, the other to examine the impacts of changes in the underlying sensitivity, specificity, and base rate information, either separately or jointly. For example, starting out with the initial values of sensitivity of 80%, specificity of 70%, and base rate of 20%, changing one or all of the top set of three sliders alters the posterior inferences—but leaves visible the reference specifications. Snapshot 1 shows the initial configuration and calculation of relevant inverse probabilities. Snapshot 2 shows the effect of varying only one parameter; here reducing the base rate reduces 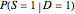significantly in the diagram and the truth table representation shows why—there are so many more false positives. Snapshot 3 shows the effect of varying another parameter; here increasing the specificity of the test increases 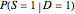significantly in the diagram and the truth table representation shows why—the number of false positives drops dramatically. Of course the reference specification itself can also be changed by changing the sliders in the lower box.

A fuller explanation of the coherency relationships involved in Bayes's theorem is available in the Demonstration "Bayes Theorem and Inverse Probability". A more descriptive explanation complete with guided webcasts and references can be found at the UCTV site.

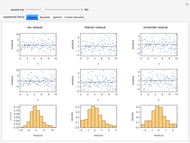
Snapshot 1: a basic starting point

Snapshot 2: changing the base rate

Snapshot 3: changing the specificity