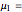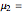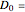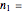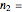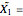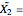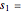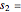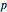Comparing Two Means Using Independent Samples of Unknown Variance
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
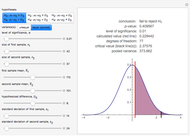
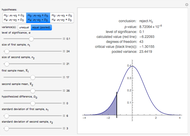
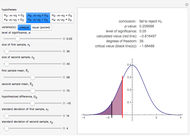
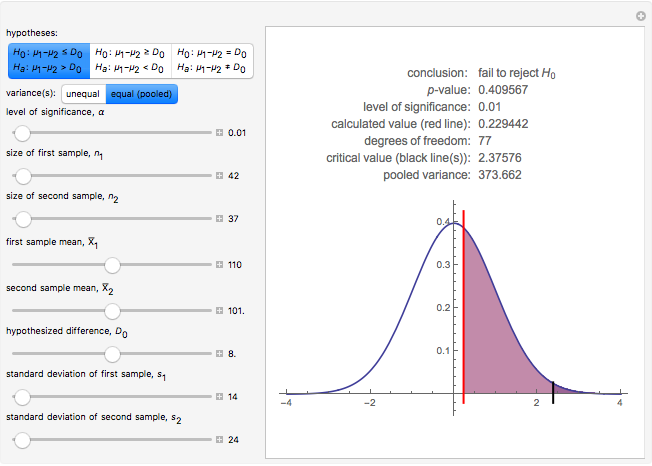
This Demonstration illustrates the hypotheses testing of the means of two independent populations with unknown variances, based on independent samples. These are the parameters used in this example:
[more]
Contributed by: Shailesh S. Kulkarni and Hakan Tarakci (December 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] A. H. Kvanli, R. J. Pavur and K. B. Keeling, Business Statistics: Analytics for Decision Making, Stamford, CT: Cengage Learning, 2010.
Permanent Citation