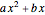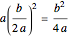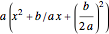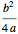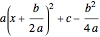Completing the Square
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
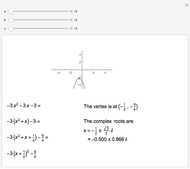
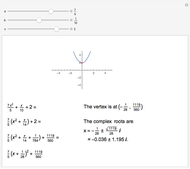
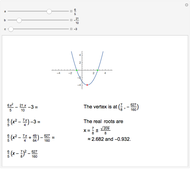
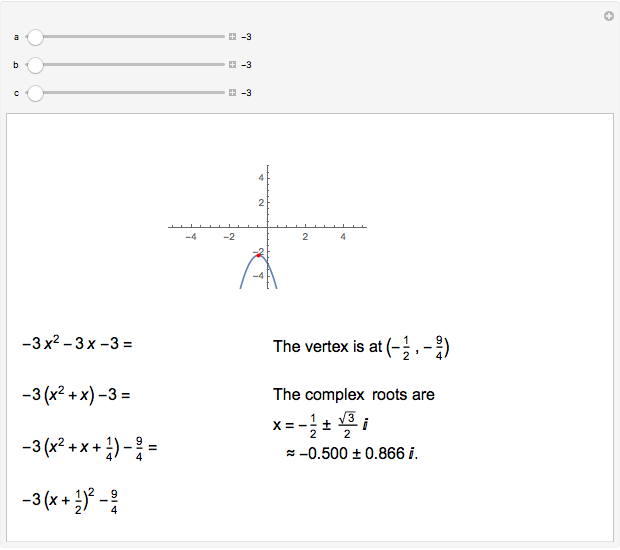
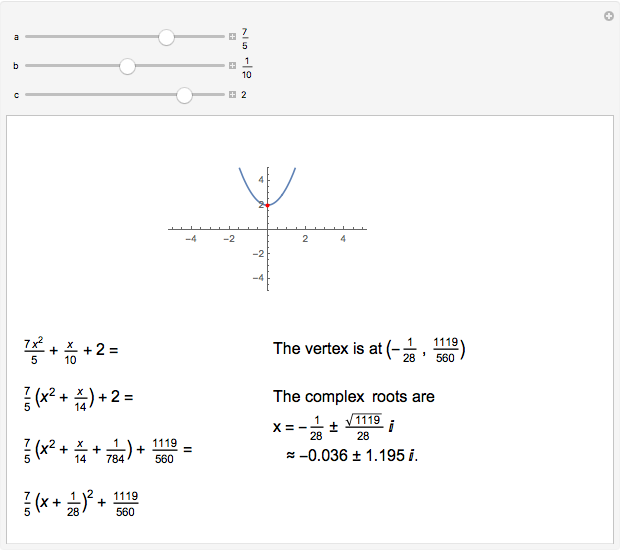
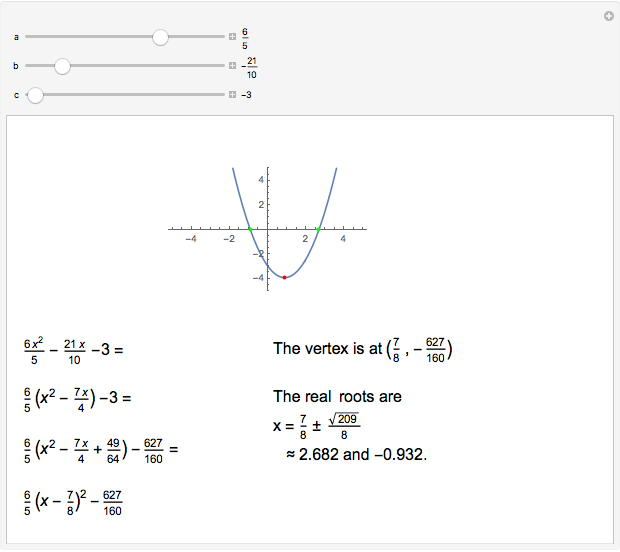
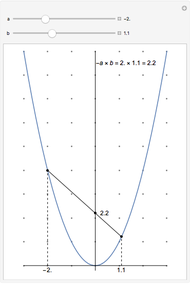
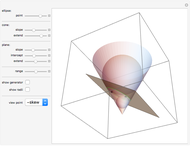
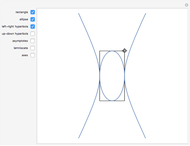
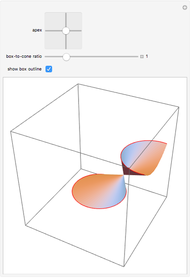
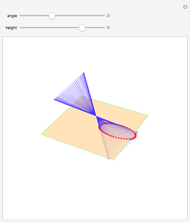
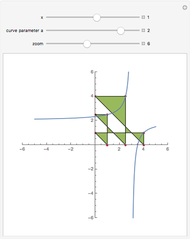
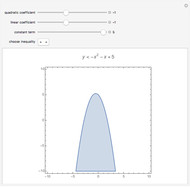
Completing the square of a quadratic function 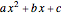 is useful for solving the equation
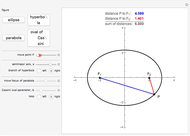
is useful for solving the equation 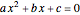 , for plotting the graph of the function, or for finding the center of the circle (or other conic section) that is the graph of
, for plotting the graph of the function, or for finding the center of the circle (or other conic section) that is the graph of 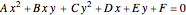 .
.
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In calculus, completing the square lets you use substitution to change integrals involving quadratics to some standard form. For example,
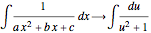 and
and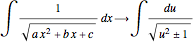 or
or 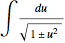 .
.
Permanent Citation