Computed Tomography Simulation Using the Radon Transform

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
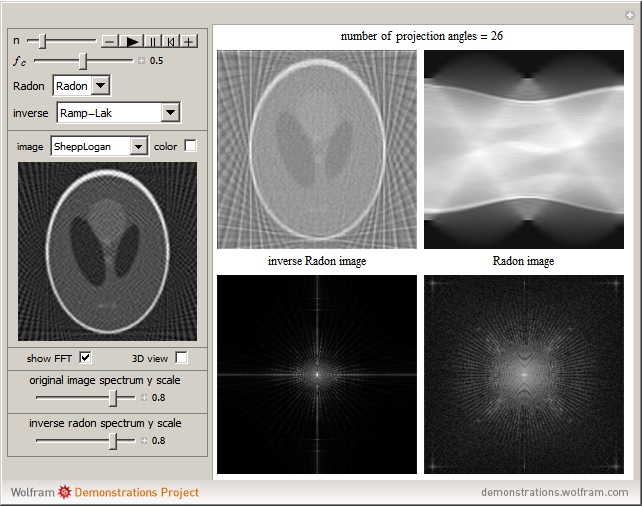
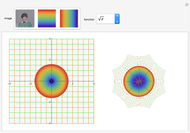
This Demonstration illustrates computed tomography (CT). It applies the Radon transform on the selected image with a number of projection angles. Using the inverse Radon transform on the resulting Radon image shows that the reconstructed image starts to resemble the original image as the number of projection angles increases.
Contributed by: Nasser M. Abbasi (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The larger the number of projections applied on the original image, the more accurate the reconstructed image becomes. In computed tomography, many projections of the object are first generated from different angles. Then filtered back-projections are applied to reconstruct a 2D image of the structure of a particular cross section of the image. This is the basic idea used in X-ray medical imaging.
The Radon transform and the inverse Radon transform (both added in Mathematica 8) are used to simulate this method. Up to 128 projections can be taken between  . Then applying the inverse Radon transform on the resulting image gives the filtered back-projection image.
. Then applying the inverse Radon transform on the resulting image gives the filtered back-projection image.
In this Demonstration, only one filtered back projection is used per projection. The magnitude spectrum of the reconstructed image (the inverse Radon image) is updated as more back projections are applied, showing that the spectrum approaches that of the original image. Ram–Lak and cosine ramp filters for inverse Radon transform generate the clearest reconstruction; however, streak lines appear across the reconstructed image; these do not appear in some of the other filters nor for the nonfiltered image.
The "n" slider represents the number of projections or angles to apply. The parameter  is Mathematica's "CutoffFrequency" option for the inverse Radon. You can adjust the 2D frequency spectrum of the images for better viewing. A checkbox lets you change the view of the image magnitude spectrum from 2D to 3D. For original color images, a checkbox can be used to process the image in gray only, as processing the image in color requires more time and memory.
is Mathematica's "CutoffFrequency" option for the inverse Radon. You can adjust the 2D frequency spectrum of the images for better viewing. A checkbox lets you change the view of the image magnitude spectrum from 2D to 3D. For original color images, a checkbox can be used to process the image in gray only, as processing the image in color requires more time and memory.
For more information, see the website on the window function and the author's report on computed tomography.
References
[1] A. C. Kak and M. Slaney, Principles of Computerized Tomographic Imaging, New Brunswick, NJ: IEEE Press, 1988.
[2] H. Murrell, "Computer-Aided Tomography," The Mathematica Journal, 6(2), 1996 pp. 60–65.
Permanent Citation