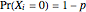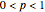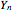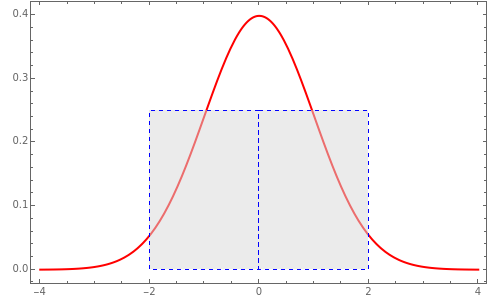
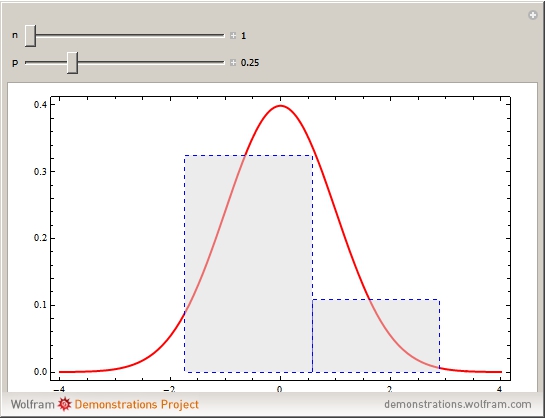
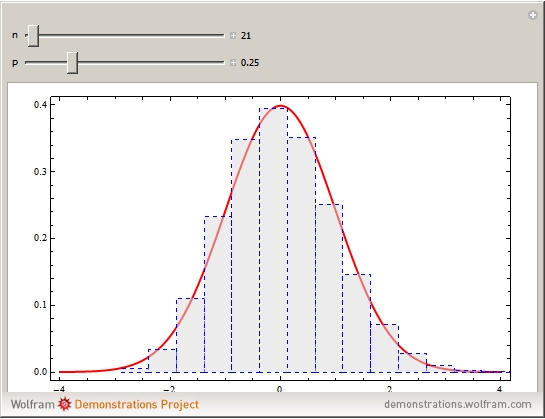
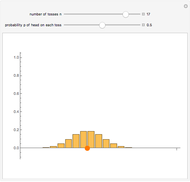
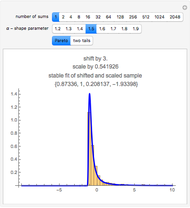
Consider the central limit theorem for independent Bernoulli random variables , where and , . Then the sum is binomial with parameters and and converges in distribution to the standard normal. The exact distribution for may be written , where , , . The convergence may be illustrated using rectangles of width 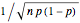and height centered at . As increases, the rectangles closely approach the standard normal density function. The convergence is faster in the symmetric case when .