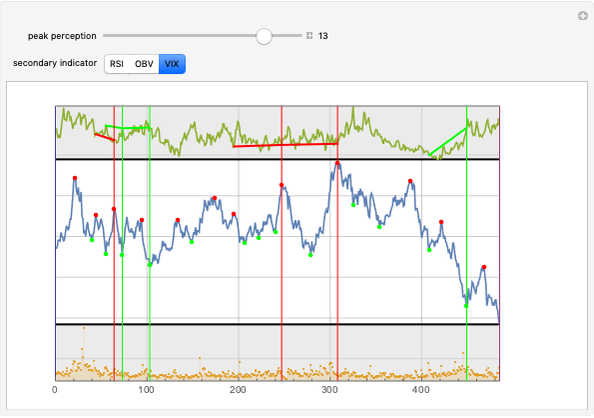
Constant Price Elasticity of Demand

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
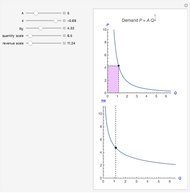
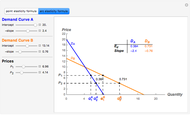
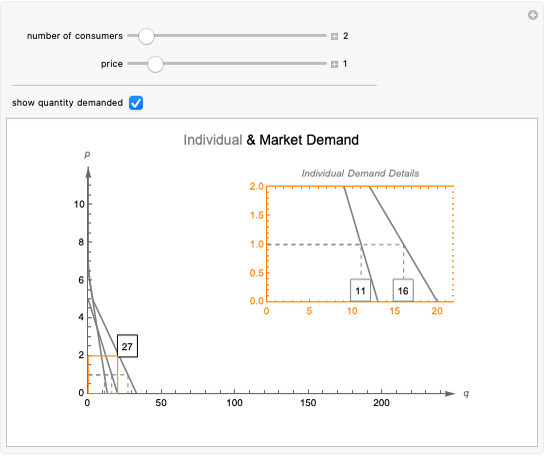
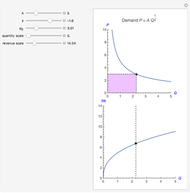
The inverse demand function  has a constant price elasticity of demand
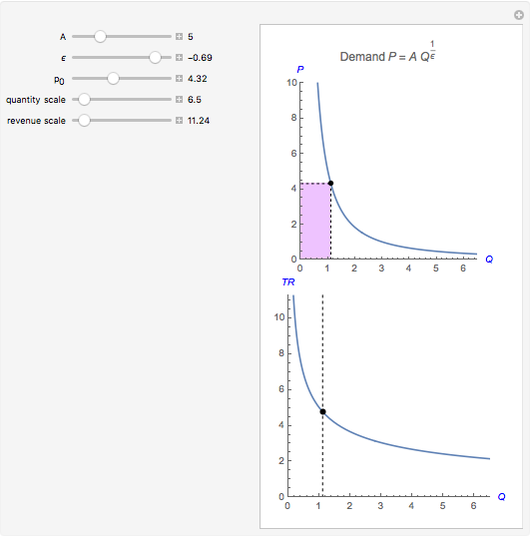
has a constant price elasticity of demand  . The revenue is shown as an area in the upper quadrant and is also plotted as the height of the function in the lower quadrant. As the price falls, the revenue area decreases for inelastic demand (
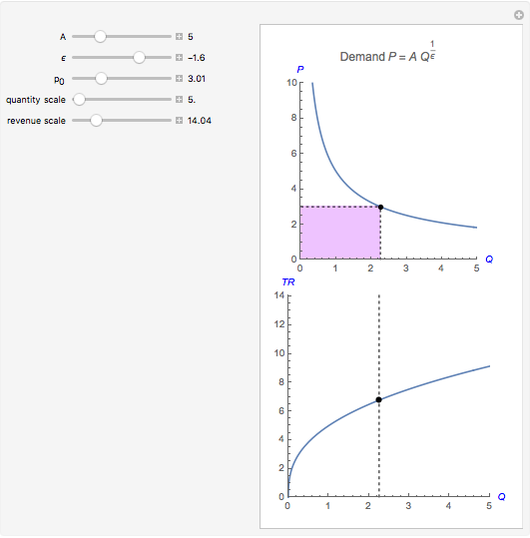
. The revenue is shown as an area in the upper quadrant and is also plotted as the height of the function in the lower quadrant. As the price falls, the revenue area decreases for inelastic demand ( ), remains constant for unit elastic demand (
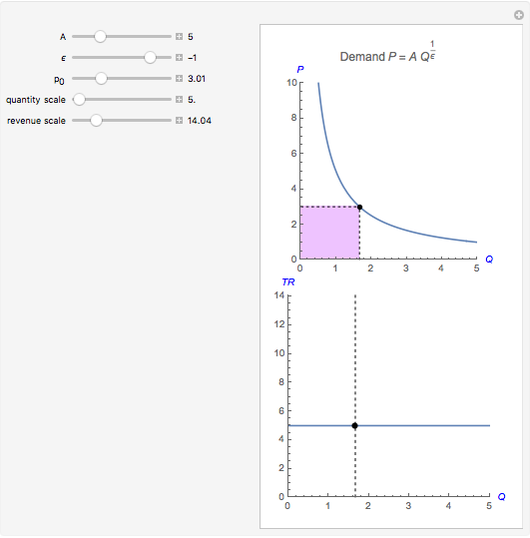
), remains constant for unit elastic demand ( ), and increases for elastic demand (
), and increases for elastic demand ( ).
).
Contributed by: Craig Marcott (February 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: elastic demand
Snapshot 2: unit elastic demand
Snapshot 3: inelastic demand
The price elasticity of demand is the percentage change in quantity demanded divided by the percentage change in price:  .
.
An inverse demand function of the form  has a constant price elasticity of demand
has a constant price elasticity of demand  . To show this, take natural logs and differentiate, treating
. To show this, take natural logs and differentiate, treating  and
and  as constants.
as constants.
Solving for  gives
gives  .
.
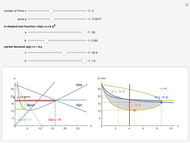
Many times students and instructors assume linear forms for supply and demand. A justification for this assumption might be that if one is primarily interested in simple quantitative predictions about the comparative static effects of events on price and quantity, one should not add auxiliary assumptions about the shapes of the curves; a rule of parsimony supports using the simplest functional form (i.e., linear) that will get the job done. Another justification for linearity assumptions is that they are easy to work with when algebraic solutions are sought.
This inverse demand function is used in [1] to show how linearity assumptions can sometimes lead to misleading conclusions. It can be shown that the following relationship between elasticity and marginal revenue ( ) always holds:
) always holds:  . Set this equal to
. Set this equal to  and solve for a profit-maximizing markup pricing rule:
and solve for a profit-maximizing markup pricing rule: 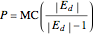 . With the constant price elasticity of demand function used in this Demonstration, the markup pricing rule is
. With the constant price elasticity of demand function used in this Demonstration, the markup pricing rule is  .
.
Now suppose the government imposes a tax of  on a monopolist with this constant elasticity form of demand. Since price searchers always produce in the elastic region of the demand curve,
on a monopolist with this constant elasticity form of demand. Since price searchers always produce in the elastic region of the demand curve,  . This means a monopolist or a monopolistic competitor has an optimal strategy of passing more than 100% of the tax on to consumers of the good (i.e.,
. This means a monopolist or a monopolistic competitor has an optimal strategy of passing more than 100% of the tax on to consumers of the good (i.e.,  implies
implies  ). For example, if
). For example, if  is a monopolist's constant price elasticity of demand and the government imposes a per unit tax of $1 on the firm, then this rascal will increase its price by $2.
is a monopolist's constant price elasticity of demand and the government imposes a per unit tax of $1 on the firm, then this rascal will increase its price by $2.
Contrast this unsettling public policy result with the more comforting conclusions associated with an assumption of linear demand. In this linear case, marginal revenue is also linear and is twice as steep as demand. A monopolist with constant (i.e., horizontal) marginal cost would pass on half of the per unit tax to consumers (i.e.,  ). If
). If  is upward-sloping, then the monopolist passes on less than half of the tax.
is upward-sloping, then the monopolist passes on less than half of the tax.
Reference
[1] H. R. Varian, Intermediate Microeconomics with Calculus: A Modern Approach, New York: W. W. Norton & Company, 2014.
Permanent Citation