Elasticity Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
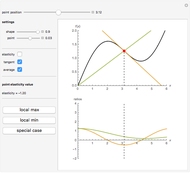
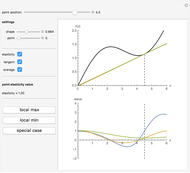
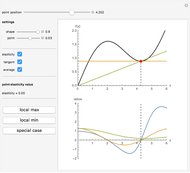
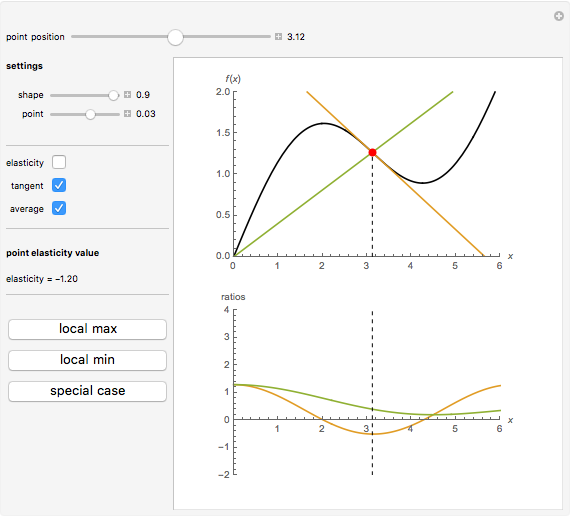
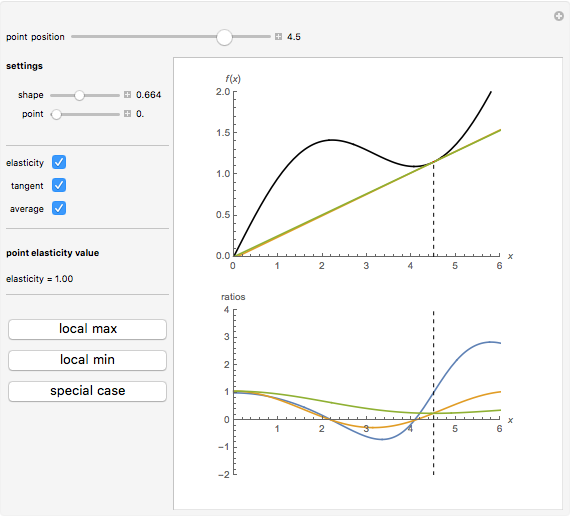
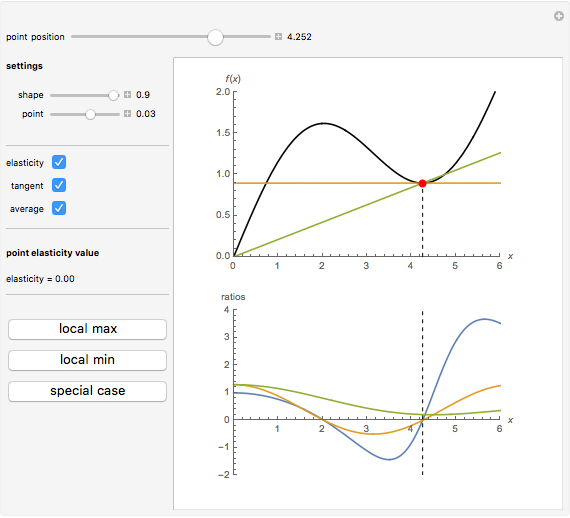
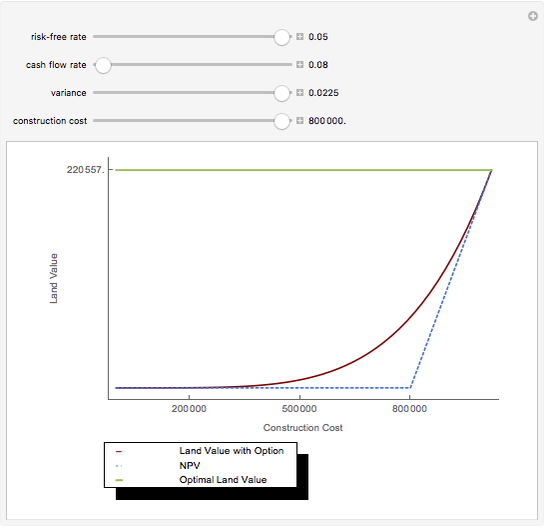
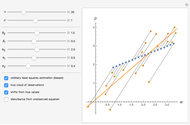
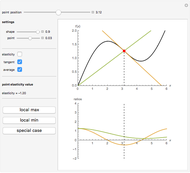
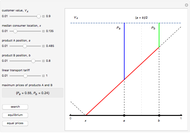
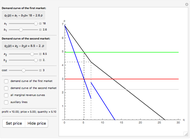
This Demonstration considers elasticity, which is one of the central concepts in theoretical and empirical economics. Elasticity is indispensable because it shows relative (per cent) change of a given variable due to relative (per cent) change in another variable. We use a smooth non-negative function  to demonstrate some useful properties of elasticity analysis. Visualization of different ratios, which are usually treated analytically, can be instructive for better understanding of elasticity and related economic concepts—for example, elasticity of demand function.
to demonstrate some useful properties of elasticity analysis. Visualization of different ratios, which are usually treated analytically, can be instructive for better understanding of elasticity and related economic concepts—for example, elasticity of demand function.
Contributed by: Timur Gareev (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
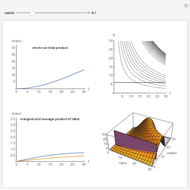
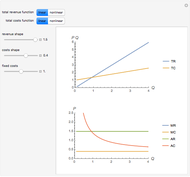
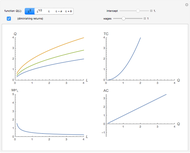
Elasticity is a function  that can be built from an arbitrary function
that can be built from an arbitrary function  . Elasticity at a certain point is usually calculated as
. Elasticity at a certain point is usually calculated as
 .
.
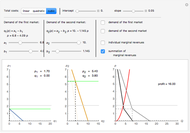
We have chosen  , as it has two inflection points (local minimum and local maximum), and also sections that slope up and down. As long as we have four terms on the right-hand side of the above expression, elasticity can be expressed in many forms. One interesting form, from an economic viewpoint, is the ratio of slopes of tangent and average curves that are shown on the upper plot:
, as it has two inflection points (local minimum and local maximum), and also sections that slope up and down. As long as we have four terms on the right-hand side of the above expression, elasticity can be expressed in many forms. One interesting form, from an economic viewpoint, is the ratio of slopes of tangent and average curves that are shown on the upper plot:
 .
.
The bottom plot reflects all three functions: average  , tangent
, tangent  and elasticity itself for a given
and elasticity itself for a given  . For each
. For each  , the elasticity function defines elasticity values for each point of
, the elasticity function defines elasticity values for each point of  . Notice that the average line in our example is always non-negative. At inflection points the tangent is zero, as is the elasticity. Elasticity is negative for the downward-sloping section of
. Notice that the average line in our example is always non-negative. At inflection points the tangent is zero, as is the elasticity. Elasticity is negative for the downward-sloping section of  .
.
Permanent Citation