Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Damped Spherical Spring Pendulum

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

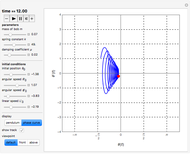
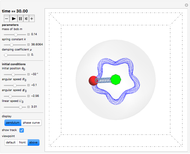
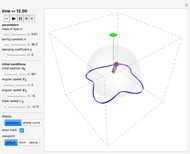
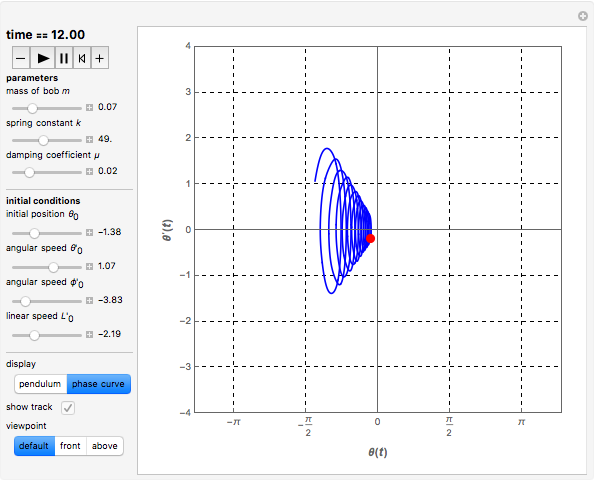
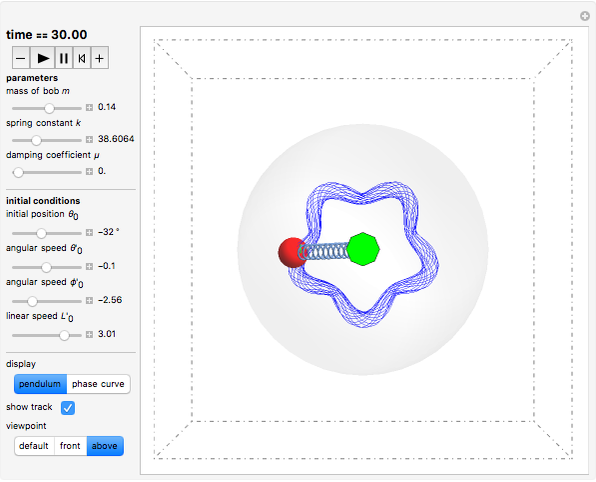
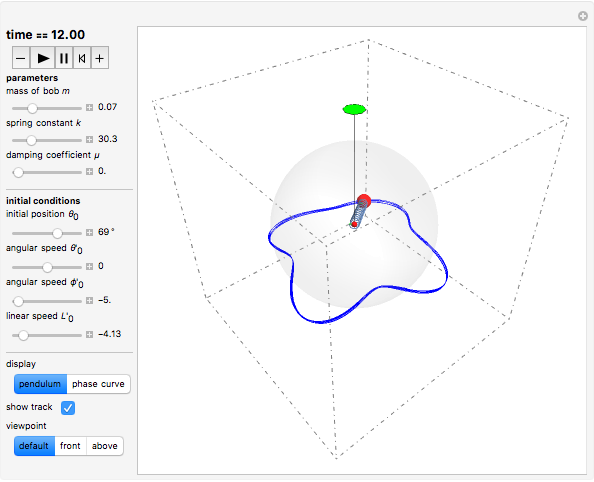
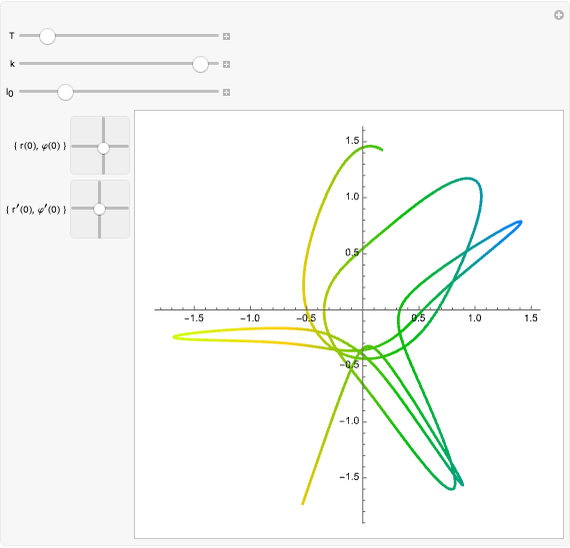
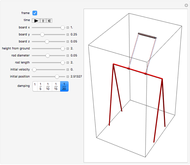
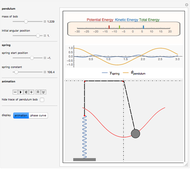
A damped spherical spring pendulum consists of a bob suspended by a spring from a fixed pivot. This Demonstration traces the path of the bob.

[more]

This system has the following three degrees of freedom: the length of the spring and the spherical coordinates of the center of the bob, and .

The three equations of motion are:

,

,

,

where is the mass of the bob and is the damping coefficient of the system.

Among the many chaotic tracks, the phase curves show many interesting periodic orbits, obtained by changing the parameters of the system.

[less]

Contributed by: Erik Mahieu (October 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The equations of motion are similar to those of the damped spherical pendulum with one additional degree of freedom, , and one more equation:

.

This equation expresses the longitudinal acceleration of the spring, which consists of four parts:

• gravity,

• spring elasticity,

• radial centrifugal force,

• tangential centrifugal force,

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send