Deriving the Labor Demand Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
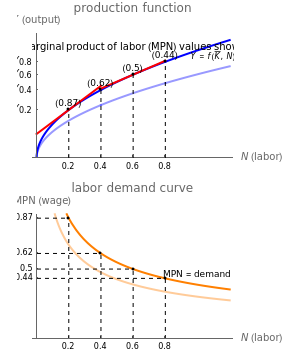
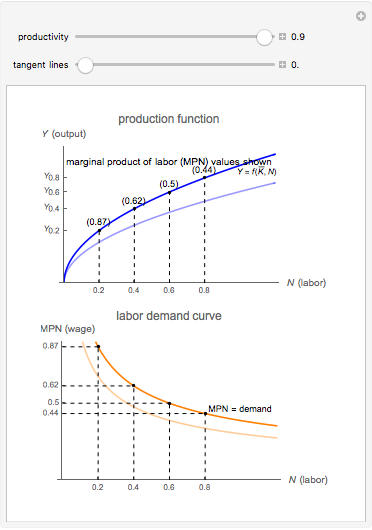
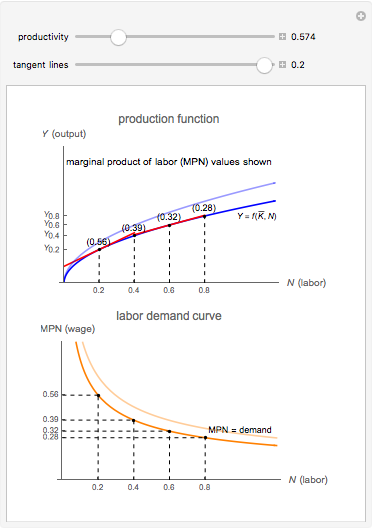
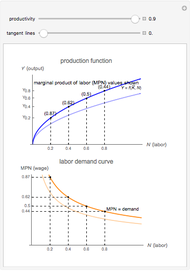
This Demonstration illustrates the origin of the labor demand curve. A firm facing a fixed amount of capital  has a logarithmic production function in which output
has a logarithmic production function in which output  is a function of the number of workers
is a function of the number of workers  . The marginal product of labor (MPN) is the amount of additional output generated by each additional worker. In other words, MPN is the derivative of the production function with respect to number of workers,
. The marginal product of labor (MPN) is the amount of additional output generated by each additional worker. In other words, MPN is the derivative of the production function with respect to number of workers,  .
.
Contributed by: Nicholas Palmer (April 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If the firm has a fixed amount of capital, its only variable input is labor. The marginal cost (MC) of labor is the wage and the marginal revenue (MR) for labor is the MPN, because that is the amount the firm receives per unit of labor. We know that all firms maximize profit when MC = MR, or in this case when the wage = MPN. Given these conditions, the labor demand curve is simply all of these points of MPN such that for any  , the firm is willing to pay the corresponding MPN as a wage because that is how the firm maximizes profit at that
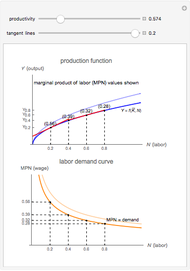
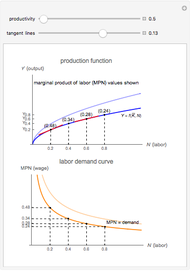
, the firm is willing to pay the corresponding MPN as a wage because that is how the firm maximizes profit at that  value. As productivity increases, MPN increases, thereby shifting the labor demand curve out, which leads to higher wages.
value. As productivity increases, MPN increases, thereby shifting the labor demand curve out, which leads to higher wages.
Permanent Citation