Details

Usually the belt trick is done with a playing card, book, or doll attached to the ribbon's free end so that one can keep track of the number of turns imparted on the free end. Looping the belt over the doll adds two full twists to the belt, and whether the belt is looped over the doll left to right or right to left defines the sense of these twists. Why there are two twists rather than one should be clear from the middle half of the simulation: each of the sides of the loop work as swivels and take up a twist of two full turns in allowing the ribbon to be looped over the doll. 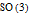The belt trick works because the evolution of the Serret–Frenet frames along the twisted ribbon encodes a continuous path through from the identity to the transformation defined by the doll's orientation in space, and so the ribbon precisely encodes the homotopy class of this path. If you can loop it over the doll (deform the path continuously) and undo the twists, the ribbon is still encoding the same homotopy class. The belt trick is a precise physical analogy to the mathematical procedure for building a universal cover. 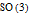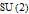The humble observation about the relationship between and explains all the following:

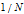
1. There are no other spin-1/3, or any aside from 1/2, ribbons realizable in a Dirac belt trick.

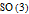
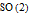
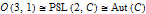
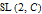
2. Spinors and tensors exhaust the list of everything that transforms compatibly with rotations. Actually the idea broadens from the with relationship to general proper Lorentz transformations: we add boosts to the mix and get the identity-connected component of the Lorentz group (the latter being the group of invertible Möbius transformations) and the double cover of this beast is , so spinors and tensors exhaust the list of everything that transforms compatibly with rotations, boosts, and general combinations thereof.

3. There are only bosons and fermions (that is, only particles with half-integer or whole-number spins) in the world.

An excellent reference for the global topology of Lie groups and the relationship between groups with the same Lie algebra is given in chapter 8 of [2].

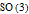
See the discussion of the two Lie groups (group of ordinary rotations in 3D space) and its universal (double) cover, for example, at [1].

For a more graceful movie of the infinite Dirac belt see the Motion Mountain Physics video page[5]; however, the explicity homotopy shown in the present demonstration whereby the belt twists are squeezed into the "vertical" parts of the belt system shows their actions as "swivvels" to allow the twist to be undone homotopically without shifting the doll (spinorial object). The exact transformations on the belt are harder to grasp in the more graceful video.

References

[1] Stack Exchange, "Quantum Field Theory—Lie Groups and Group Extensions?" (Sept 4, 2013) physics.stackexchange.com/a/76191/26076.

[2] J. Stillwell, Naïve Lie Theory, New York: Springer, 2010.

[3] W. Rossmann, Lie Groups: An Introduction through Linear Groups (Oxford Graduate Texts in Mathematics), Oxford: Oxford University Press, 2003.

[4] J. F. Adams, Lectures on Lie Groups, Chicago: The University of Chicago Press, 1983.

[5] Motion Mountain Physics, "Fascinating Physics Videos" (retrieved Nov 19, 2013) motionmountain.net/videos.html and, explicitly, vimeo.com/62228139