The Banach-Tarski Paradox

Initializing live version

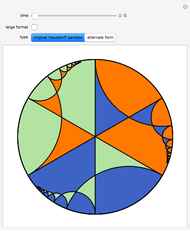
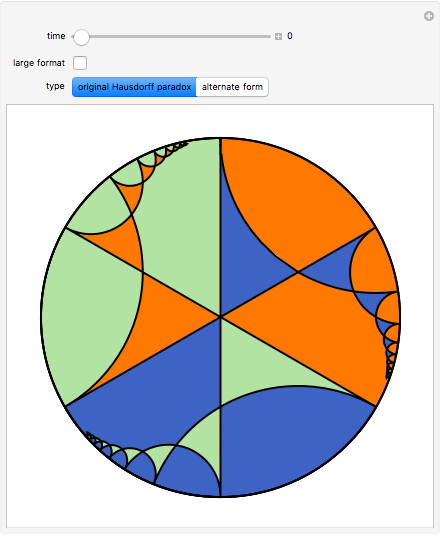
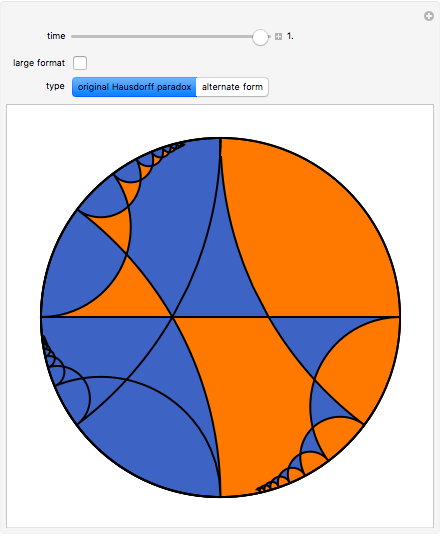
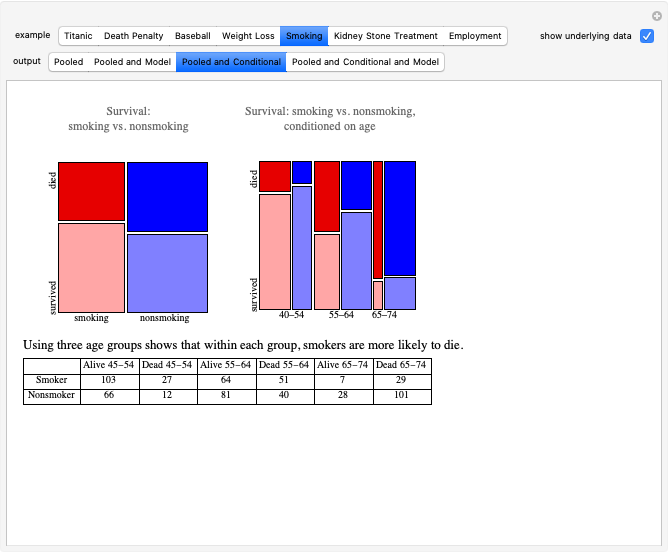
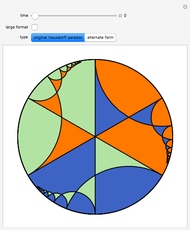
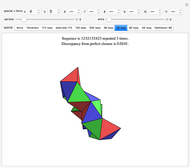
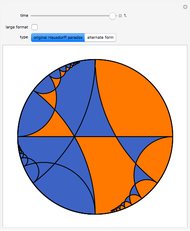
This Demonstration shows a constructive version of the Banach–Tarski paradox, discovered by Jan Mycielski and Stan Wagon. The three colors define congruent sets in the hyperbolic plane , and from the initial viewpoint the sets appear congruent to our Euclidean eyes. Thus the orange set is one third of . But as we fly over the plane to a new viewpoint, we come to a place where the congruence of orange to the green and blue combined becomes evident. Thus the orange is now half of .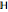

Contributed by: Stan Wagon (April 2007)
(Macalester College)
Open content licensed under CC BY-NC-SA

Snapshots

Details

(*) , , .

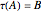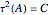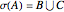Snapshot 1: the orange set is a third of the hyperbolic plane

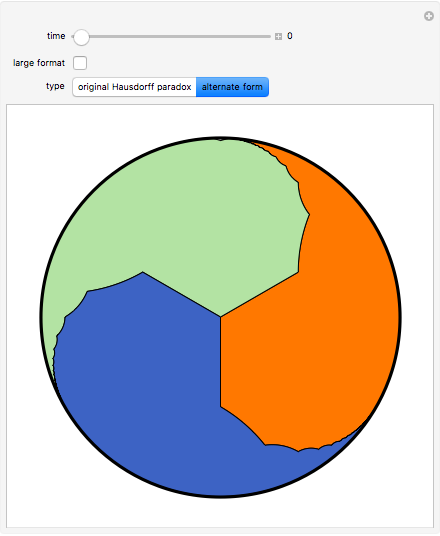
Snapshot 2: the viewpoint has switched and the green region has become blue; the orange set is now congruent to the green and blue combined, and so is one half of the hyperbolic plane

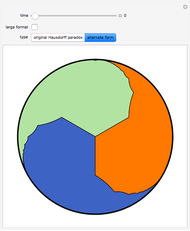
Snapshot 3: the orange set in the alternative paradox is a little simpler, and is still simultaneously a third and a half of the hyperbolic plane

More details can be found in [1].

Reference

[1] S. Wagon, The Banach-Tarski Paradox, New York: Cambridge University Press, 1985.

Permanent Citation

Stan Wagon "The Banach-Tarski Paradox"
http://demonstrations.wolfram.com/TheBanachTarskiParadox/
Wolfram Demonstrations Project
Published: April 27 2007


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send

The Banach-Tarski Paradox

Snapshots

Details

Related Links

Permanent Citation