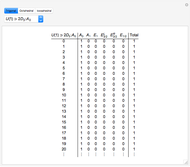
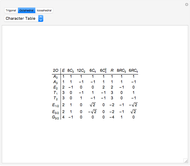
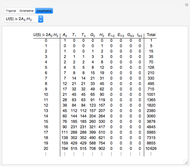
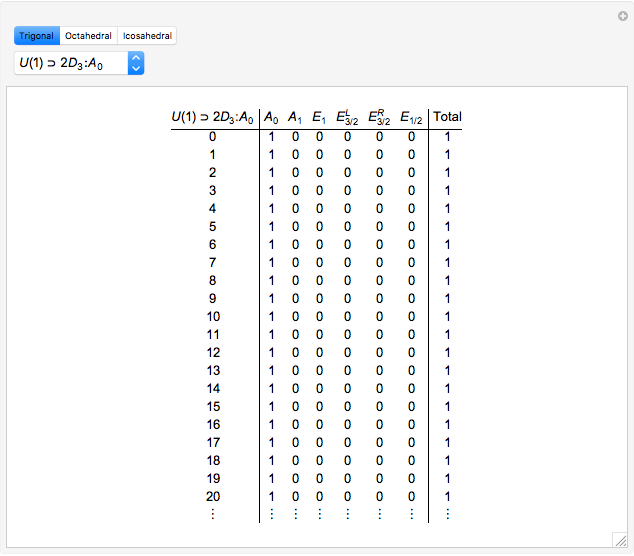
Molien Series for a Few Double Groups

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
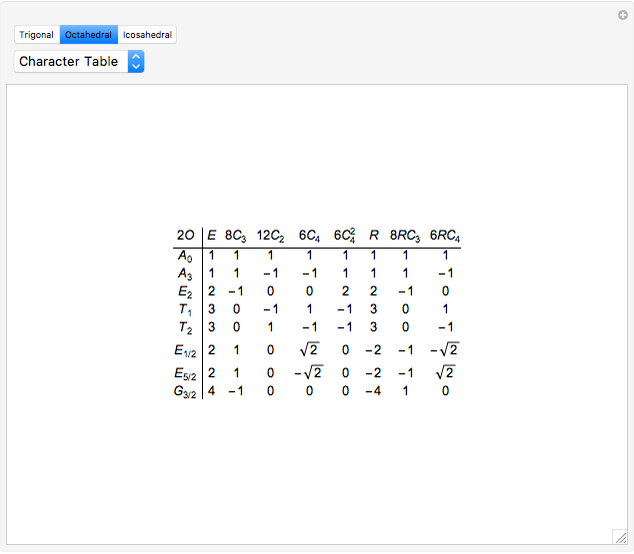
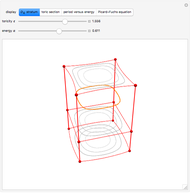
The Molien equation [1, 2] determines symmetry correlation tables [3]. The tables presented here describe correlations between representations of the unitary group and various finite subgroups: double trigonal  , double octahedral
, double octahedral  , and double icosahedral
, and double icosahedral  . In the history of science, double groups were introduced by Klein [4] and subsequently applied to physics by Bethe [5]. Both German works are available in English.
. In the history of science, double groups were introduced by Klein [4] and subsequently applied to physics by Bethe [5]. Both German works are available in English.
Contributed by: Brad Klee (February 2016)
Open content licensed under CC BY-NC-SA
Details
Classical invariant theory applies whenever a finite symmetry group  imposes constraints on a function
imposes constraints on a function  that admits a multidimensional power series expansion. Math, physics, and computer science provide many great examples where century-old theorems can be put to good use [1]. The complete mathematical theory is difficult to understand and operate, but calculating Molien generating functions is relatively simple. A proof of the Molien equation requires only basic representation theory: character tables, representation induction, and idempotent projectors.
that admits a multidimensional power series expansion. Math, physics, and computer science provide many great examples where century-old theorems can be put to good use [1]. The complete mathematical theory is difficult to understand and operate, but calculating Molien generating functions is relatively simple. A proof of the Molien equation requires only basic representation theory: character tables, representation induction, and idempotent projectors.
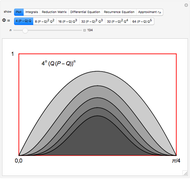
The Molien equation is
 ,
,
where the sum is taken over all  in the representation
in the representation  of the symmetry group
of the symmetry group  .
.
The variables are defined as follows:
The argument  is a representation of the symmetry group
is a representation of the symmetry group  that transforms coordinates
that transforms coordinates  , which thus determines a unique correlation table.
, which thus determines a unique correlation table.
 is an irreducible representation of
is an irreducible representation of  that determines a covariant or invariant transformation property, which thus determines a unique table column.
that determines a covariant or invariant transformation property, which thus determines a unique table column.
 is a formal variable used in the power series expansion.
is a formal variable used in the power series expansion.
 is an element of
is an element of  in the representation
in the representation  .
.
 is the identity element of
is the identity element of  in the representation
in the representation  .
.
 is the order of
is the order of  .
.
 is the character of the action
is the character of the action  in the representation
in the representation  .
.
Star (*) denotes complex conjugation.
Computational efficiency can be improved by changing the sum in the Molien function to include just one term from each class. All terms in the same class have the same determinant, as can be seen by applying a unitary transformation.
In the code, we use a Molien equation adapted to the regular representation to calculate determinants of the double octahedral group. This Molien equation differs from the standard only by the addition of an extra, fractional exponent attached to the determinant. The exponent is necessary because the regular representation contains exactly  copies of the
copies of the  representation. Understanding this fact, the adapted function can be proven correct by the same means as applied to the usual function [1, 2].
representation. Understanding this fact, the adapted function can be proven correct by the same means as applied to the usual function [1, 2].
Trigonal determinants can be computed via the regular representation. Brute force fails for icosahedral, so other methods must be used to generate each irreducible representation separately. In the code we generate trigonal and icosahedral tables from tabulated determinant functions. These are more convenient to store than the generating functions. Calculation of the generating functions from determinant polynomials is not prohibitively slow. It is possible to compare these primitives with those published in the literature [8]. Trigonal and octahedral determinants match published results, but the results published for icosahedral symmetry in [8] contain a few obvious errors. The tables here are correct.
The sequences determined by  are conjectured to be related to sequences found in the On-Line Encyclopedia of Integer Sequences [9]. We could prove the tabulated identities by comparing generating functions. However, it is highly likely that all relations are correct. These sequences are known to be linear recurrences, which are easy to match in term-by-term searches. Although most of the sequences are already known, those marked A?????? appear to be missing from OEIS as of February 2, 2016.
are conjectured to be related to sequences found in the On-Line Encyclopedia of Integer Sequences [9]. We could prove the tabulated identities by comparing generating functions. However, it is highly likely that all relations are correct. These sequences are known to be linear recurrences, which are easy to match in term-by-term searches. Although most of the sequences are already known, those marked A?????? appear to be missing from OEIS as of February 2, 2016.
References
[1] N. J. A. Sloane, "Error-Correcting Codes and Invariant Theory: New Applications of a Nineteenth-Century Technique," The American Mathematical Monthly, 84(2), 1977 pp. 82–107. doi:10.2307/2319929.
[2] R. P. Stanley, "Invariants of Finite Groups and Their Applications to Combinatorics," Bulletin of the American Mathematical Society, 1(3), 1979 pp. 475–511. doi:S0273-0979-1979-14597-X.
[3] B. Klee, doctoral dissertation, forthcoming.
[4] F. Klein, Vorlesungen über das Ikosaeder: und die Auflösung der Gleichungen vom fünften Grade, Liepzig: Teubner, 1884.
[5] H. A. Bethe, "Termaufspaltung in Kristallen," Annalen der Physik, 395(2), 1929 pp. 133–208. doi:10.1002/andp.19293950202.
[6] W. G. Harter, Principles of Symmetry, Dynamics, and Spectroscopy, New York: Wiley, 1993 pp. 385 and 414.
[7] K. Balasubramanian, "Double Group of the Icosahedral Group ( ) and Its Application to Fullerenes," Chemical Physics Letters, 260(3), 1996 pp. 476–484. doi:10.1016/0009-2614(96)00849-4.
) and Its Application to Fullerenes," Chemical Physics Letters, 260(3), 1996 pp. 476–484. doi:10.1016/0009-2614(96)00849-4.
[8] P. E. Desmier and R. T. Sharp, "Polynomial Tensors for Double Point Groups," Journal of Mathematical Physics, 20(1), 1979 pp. 74–82. doi:10.1063/1.523932.
[9] N. J. A. Sloane. "The On-Line Encyclopedia of Integer Sequences." (Feb 2, 2016) oeis.org.
Snapshots
Permanent Citation