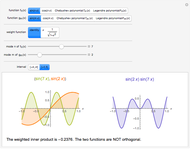
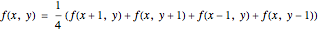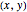Discrete Harmonic Functions and Dirichlet's Relaxation Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Discrete harmonic functions are derived from harmonic functions (i.e. solutions to the Laplace equation). More specifically, a discrete harmonic function on a two-dimensional domain 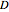 is a function
is a function  defined on the lattice points (i.e. points with integer coordinates) of
defined on the lattice points (i.e. points with integer coordinates) of 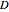 that satisfies the discrete mean-value property
that satisfies the discrete mean-value property
Contributed by: Yuheng Chang (January 2019)
Based on an undergraduate research project at the Illinois Geometry Lab by Yuheng Chang, Baihe Duan, Yirui Luo, Yitao Meng, Cameron Nachreiner and Yiyin Shen and directed by A. J. Hildebrand.
Open content licensed under CC BY-NC-SA
Details
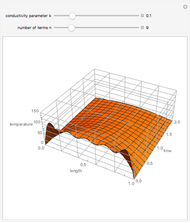
Discrete Harmonic Functions and Electric Networks
Discrete harmonic functions have a natural interpretation in the context of electric networks. Interpret the lattice points in a 2D domain as nodes of an electric network connected with resistors, and let 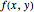 denote the voltage at the point
denote the voltage at the point 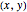 . Then the function
. Then the function  is a discrete harmonic function; see [1] for details.
is a discrete harmonic function; see [1] for details.
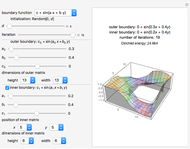
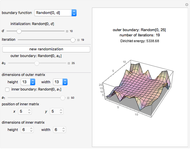
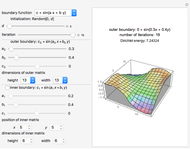
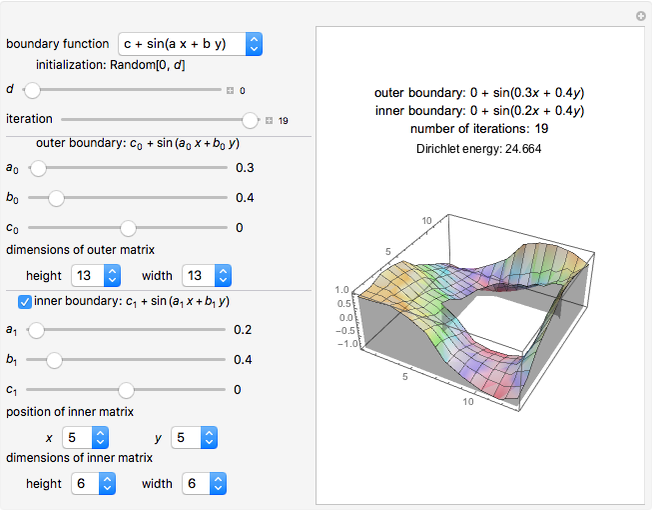
Dirichlet Method of Relaxations
This is an iterative method for computing discrete harmonic functions with given boundary values. Starting with an arbitrary initial function 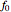 satisfying the boundary conditions, the method constructs a sequence
satisfying the boundary conditions, the method constructs a sequence 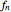 of functions defined by
of functions defined by
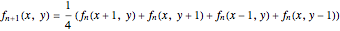 .
.
As  ,
, 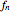 approaches a harmonic function; see [1, p. 16].
approaches a harmonic function; see [1, p. 16].
Boundary Functions
Three families of boundary functions are provided for the outer and inner (if selected) boundaries of the domain:
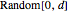 and
and
 ,
,
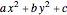 ,
,
where 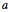 ,
,  ,
,  are user-defined parameters.
are user-defined parameters.
The values of 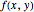 at the boundary are random real numbers chosen uniformly from the interval
at the boundary are random real numbers chosen uniformly from the interval  , where
, where
 is a user-defined parameter.
is a user-defined parameter.
Initialization
For this Demonstration, we chose to initialize the values of 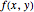 in the interior of the domain
in the interior of the domain 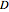 to random real numbers chosen uniformly from the interval
to random real numbers chosen uniformly from the interval 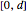 , where
, where
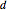 is a user-defined parameter. Choosing
is a user-defined parameter. Choosing  as 0 is equivalent to initializing the values in the interior of
as 0 is equivalent to initializing the values in the interior of 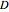 to
to  .
.
Dirichlet Energy
For continuous functions  defined on some domain
defined on some domain  , the integral
, the integral 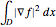 , where
, where 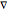 denotes the gradient, is called the Dirichlet energy integral. This integral can be interpreted as the potential energy of a system or as a measure of the "energy" of the surface
denotes the gradient, is called the Dirichlet energy integral. This integral can be interpreted as the potential energy of a system or as a measure of the "energy" of the surface  . The smaller this integral, the flatter the surface. A characteristic property of harmonic functions is that they minimize the Dirichlet energy integral. From among all functions having given values on the boundary of
. The smaller this integral, the flatter the surface. A characteristic property of harmonic functions is that they minimize the Dirichlet energy integral. From among all functions having given values on the boundary of 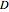 , the harmonic function satisfying the given boundary conditions is the unique function that minimizes the Dirichlet energy integral.
, the harmonic function satisfying the given boundary conditions is the unique function that minimizes the Dirichlet energy integral.
The discrete analog of the Dirichlet energy integral is the sum over the squares of the differences of values of  on all pairs of neighboring points; that is
on all pairs of neighboring points; that is
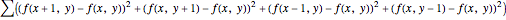 ,
,
where the sum runs over all interior lattice points 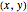 in
in 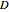 . In analogy to the continuous case, discrete harmonic functions are the unique functions that, for given boundary conditions, minimize the discrete Dirichlet energy.
. In analogy to the continuous case, discrete harmonic functions are the unique functions that, for given boundary conditions, minimize the discrete Dirichlet energy.
Reference
[1] P. G. Doyle and J. L. Snell, Random Walks and Electric Networks, Washington, DC: Mathematical Association of America, 1984.
Snapshots
Permanent Citation