Solutions of the Finite Difference Discretized Laplace Equation

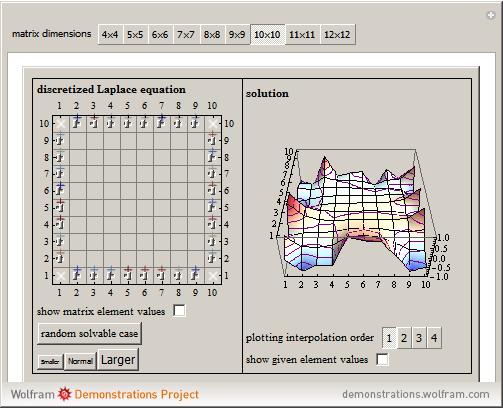
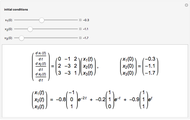
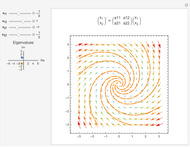
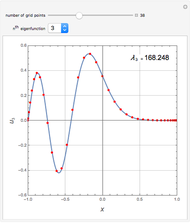
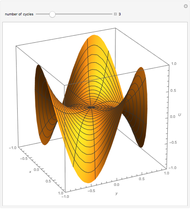
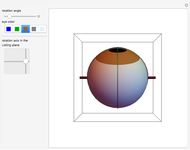
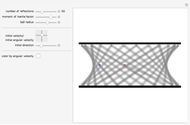
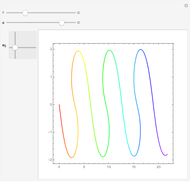
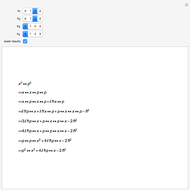
This Demonstration shows the dependence of the solution of the finite difference discretized Laplace equation on a square grid as a function of the given values at the discretization nodes.

On an square grid, the simplest finite difference approximation of the Laplace operator is . This means that generically values can be prescribed. In most textbooks, these values are on the boundary, but they can also be in the interior. Not all configurations of prescribed values are consistent. A consistent set of prescribed values leads to a unique solution.

Drag the sliders by the double arrows into any square (other than the four corners) to change the arrangement of prescribed sets of values. Use the sliders in the squares to change the values of the prescribed . (The color of the crosses indicates the values of the sliders.)