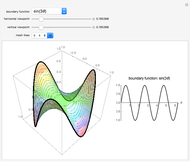
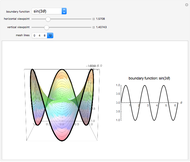
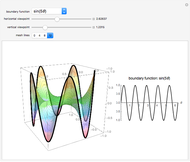
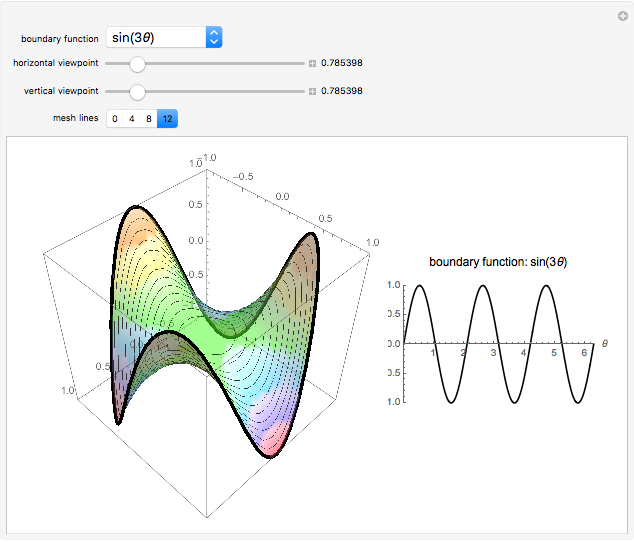
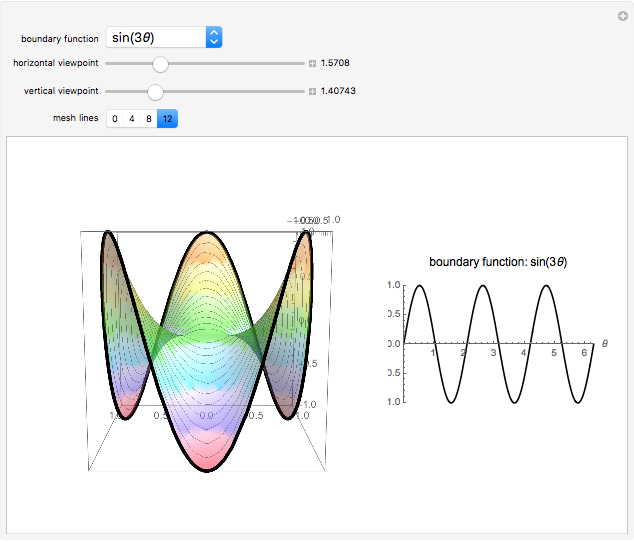
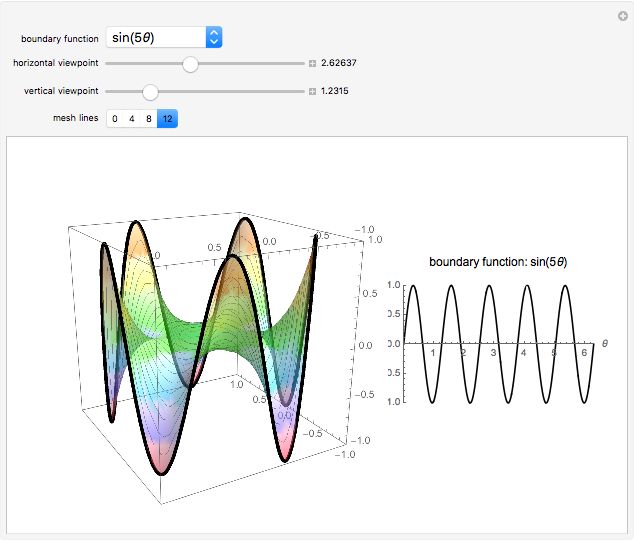
Examples of 2D Harmonic Functions
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
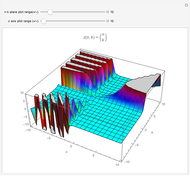
A function 
is harmonic on a domain 
if it satisfies the Laplace equation 
in the interior of 
. A remarkable property of harmonic functions is that they are uniquely defined by their values on the boundary of 
. Geometrically, this means that, given any smooth 3D curve defined on the boundary of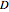 
, there exists a unique harmonic surface (i.e. a surface 
where 
is harmonic) whose boundary is the given curve.
Contributed by: Baihe Duan (January 2019)
Based on: an undergraduate research project at the Illinois Geometry Lab by Yuheng Chang, Baihe Duan, Yirui Luo, Yitao Meng, Cameron Nachreiner and Yiyin Shen, directed by A. J. Hildebrand
Open content licensed under CC BY-NC-SA
Details
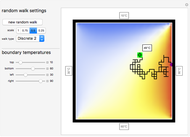
Specifying the Boundary Curve
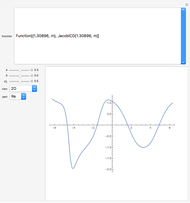
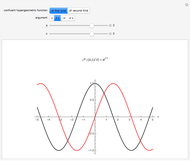
Using polar coordinates, a closed curve defined on the boundary of the unit disk can be constructed using a function 
that is periodic in 
. Therefore, specifying a boundary curve is equivalent to specifying such a periodic function 
. For the custom boundary function, a periodic Hermite interpolation of order 2 is used to match the given points (together with the points 
and 
) to a piecewise polynomial function with period 
.
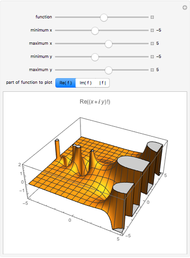
Computing the Harmonic Surface 
The values of 
in the interior of 
are computed by numerically solving the Laplace equation with the specified boundary condition.
Snapshots
Permanent Citation
Boundary Value Problem Using Series of Bessel Functions
Stephen Wilkerson
Solutions of the Elliptic Membrane Problem
Enrique Zeleny
Supersymmetric Partner Bessel Functions
N. Barbosa-Cendejas, and M. A. Reyes
Elliptic Functions
Enrique Zeleny
Spin-Weighted Spherical Harmonics
Satya Mohapatra
PolyLog Function
Enrique Zeleny
Function Explorer 3D
Ed Pegg Jr
Continuous Binomial Function in 3D
Larry Kealey
Beta Cube
Roger Bagula
Confluent Hypergeometric Functions
S. M. Blinder
