Discriminant of a Polynomial

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
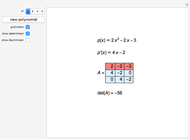
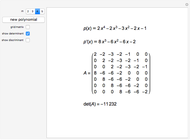
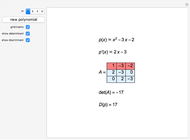
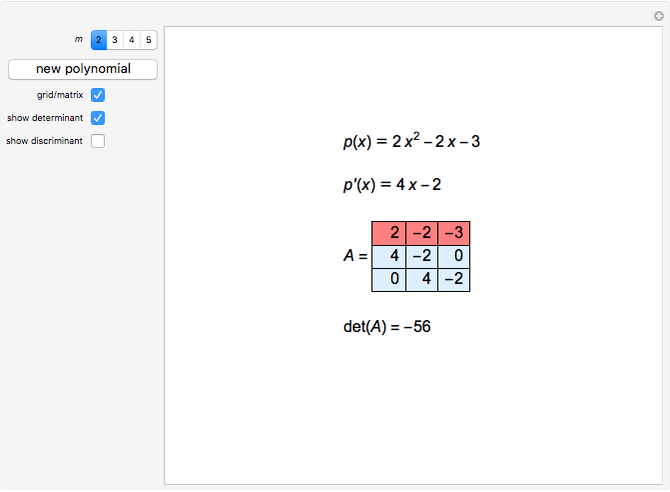
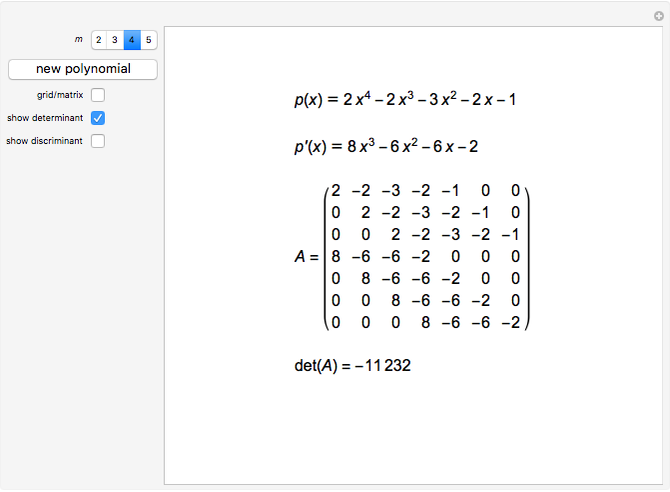
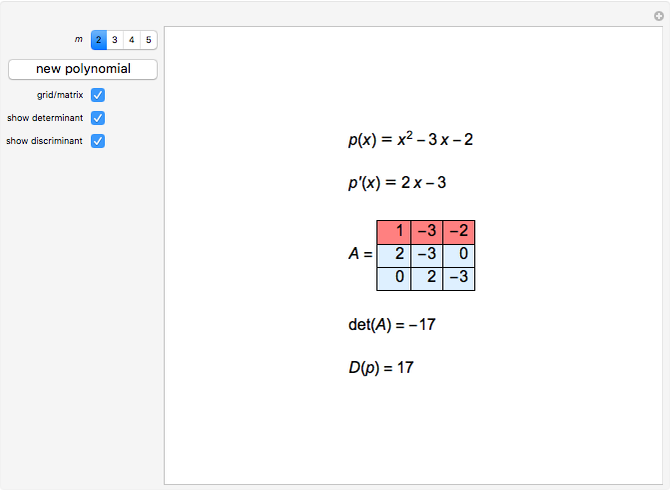
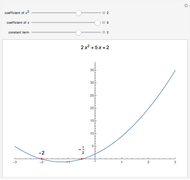
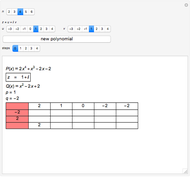
This Demonstration shows the discriminant of the polynomial  . The discriminant of a polynomial of degree
. The discriminant of a polynomial of degree  is the quantity
is the quantity  , where
, where  is the derivative of
is the derivative of  and
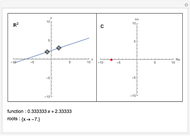
and  is the resultant of
is the resultant of  and
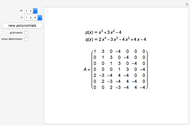
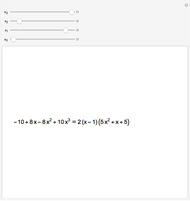
and  . The resultant is equal to the determinant of the corresponding Sylvester matrix. The discriminant of
. The resultant is equal to the determinant of the corresponding Sylvester matrix. The discriminant of  is 0 if and only if
is 0 if and only if  has a multiple root.
has a multiple root.
Contributed by: Izidor Hafner (December 2016)
Open content licensed under CC BY-NC-SA
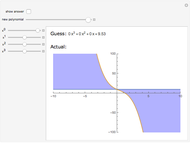
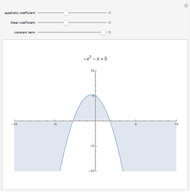
Snapshots
Details
The discriminant of a polynomial with leading coefficient 1 is the product over all pairs of roots  ,
,  of
of  .
.
The equation  relates the discriminant and resultant.
relates the discriminant and resultant.
To calculate the discriminant, we use the built-in Mathematica function Discriminant. The other way is to calculate the resultant using the Sylvester matrix and then the discriminant from the above equation.
For the meaning of the matrix/grid, see Sylvester Matrix (Wolfram MathWorld).
Reference
[1] E. J. Borowski and J. M. Borwein, Dictionary of Mathematics, London: Collins, 1989 p. 169.
Permanent Citation