Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Effect of Gravity on a Simple Pendulum

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

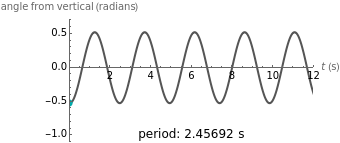
The period of a simple pendulum depends on its length and the local gravity ; at small angles, the period is given by .

[more]

This Demonstration shows how the period of a simple pendulum varies with its length and the acceleration due to gravity but independent of mass. Use the popup menu to choose preset values of gravity on different celestial bodies. Or use the sliders to vary length, gravity and mass separately.

The figure on the left displays the simple pendulum, while the figure on the right plots the position of the pendulum as a function of time. The maximum angle from the vertical is fixed at radians.

[less]

Contributed by: Julia Cai and Melinda Coleman (January 2017)
Special thanks to the University of Illinois NetMath program and the Mathematics Department at William Fremd High School.
Open content licensed under CC BY-NC-SA

Snapshots

Details

The differential equation for the angular position of an oscillating pendulum is given by .

For small angles, we can approximate , so that the equation reduces to , with solution . This corresponds to an oscillation period . A maximum angle is set for the pendulum so that the given position graph closely approximates the actual motion of an oscillating pendulum.

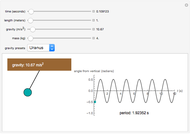
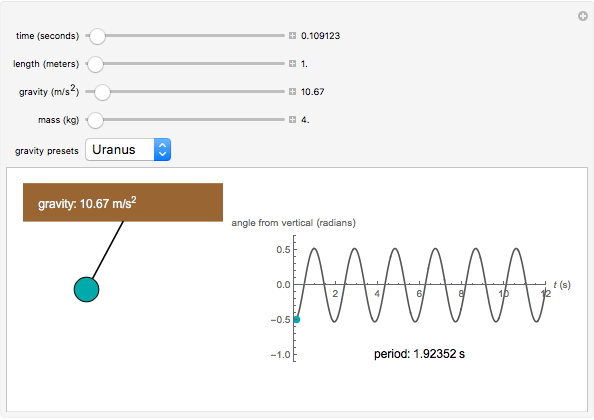
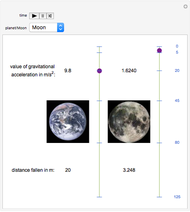
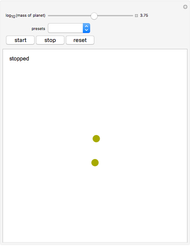
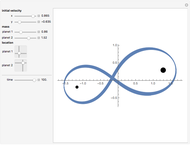
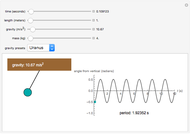
Snapshot 1: a pendulum of length 1 m and mass 4 kg on Uranus with a period of 1.924 seconds.

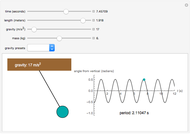
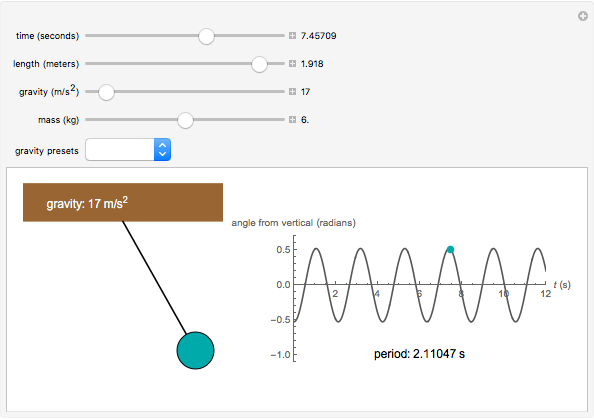
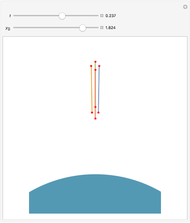
Snapshot 2: a pendulum of length 1.918 m and mass 6 kg on a planet where gravity is with a period of 2.110 s.

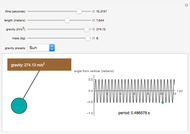
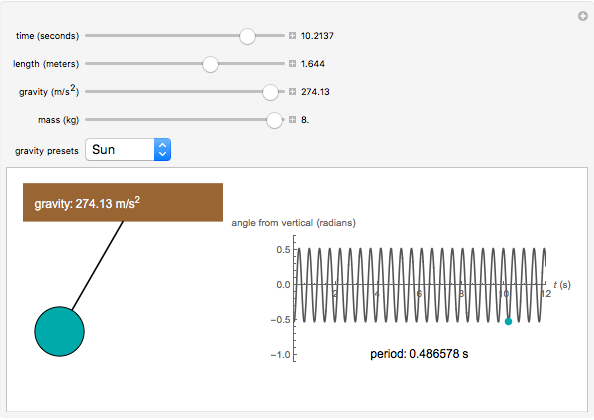
Snapshot 3: a pendulum of length 1.644 m and mass 8 kg on the Sun with a period of 0.487 s.

References

[1] R. Nave. "Simple Pendulum." (Jan 20, 2017) hyperphysics.phy-astr.gsu.edu/hbase/pend.html.

[2] J. Yoon. "Gravity on Other Planets." (Jan 20, 2017) www.aerospaceweb.org/question/astronomy/q0227.shtml.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send