Every stationary Gaussian random field 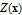 , where 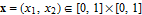 , is determined by its constant mean 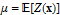 ( 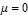 when the field is assumed centered), its variance 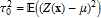 and its autocorrelation function 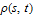 , which satisfies: This Demonstration considers a well-studied example of such a field, defined by: 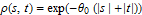 , which might be considered a simple extension of the well-known Ornstein–Uhlenbeck (OU) process to two dimensions. This random field is also called the OU sheet. As in one dimension, 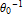 is often called the range parameter. See [1, 2] and [3, Chap. 12] for plots of the Brownian sheet, which is a limit version (as  ) of the OU sheet. Note that horizontal and vertical features are well present in an OU sheet, especially for small 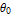 . To simplify, let us assume that one realization of such a field is observed on the regular grid 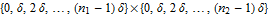 with 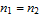 and 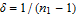 . If the observed image 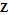 (whose 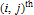 entry is 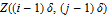 ) is rearranged in a vector 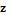 of size  by stacking its columns, it can be checked that 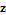 is a Gaussian vector whose covariance matrix coincides with the Kronecker product 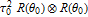 , where 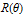 denotes the 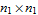 correlation matrix of an AR(1) time series of parameter 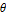 (precisely, its serial correlation being 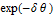 ). Such an image 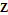 is also said to be an 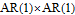 process. Simulating such a 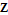 is quite fast (see Details). Here this can be done once a value for the underlying range parameter 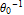 is chosen in a list of values similar to the one in Table 3 of [4], except that some smaller values are added. It is well known that the classic maximum likelihood (ML) principle can be easily implemented, even for large  , by using the known expression of  (a tridiagonal matrix) and its determinant and by exploiting the properties of the Kronecker product. It can be verified here that the calculation of the profile log-likelihood is very fast even when computed over a fine grid of 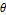 -values: this criterion (up to a constant term) multiplied by  is displayed in the top-right panel for each simulated 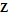 . This Demonstration also studies the "energy variance matching" alternative to ML (GE-EV method, which is the "no-noise" version of CGEM-EV), which was already implemented in a series of Demonstrations for different contexts in the one-dimensional case (Matérn autocorrelations and the powered-exponential autocorrelation). Recall that it consists of first taking the naive empirical variance 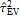 as an estimate of 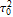 , next defining  by matching the quadratic form  , where 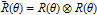 , here (the so-called "candidate Gibbs energy of 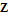 " denoted 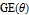 ) to 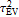 . Of course (since GE-EV requires even fewer computations than ML) the implementation of GE-EV is also very fast (bottom-right panel). As observed in [4] for isotropic random fields, ML and GE-EV methods give quite close results except for settings with a large range. For these extreme settings, the proximity of the two methods is restored provided we only focus on the estimation of the product  , which plays here the role of a micro-ergodic coefficient (see [5]), as was the case for the diffusion coefficient specific to each of the above-mentioned one-dimensional cases.
As an example, for 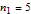 we define the following matrices: and set 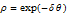 . Then the well-known expression of the inverse of 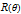 can be concisely written as:  . Then from the properties of the Kronecker product, it can be shown that  , 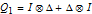 , 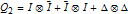 , 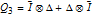 , 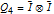 . Then, even for 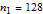 , the four  matrices 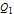 ,  , 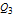 and 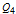 are very sparse matrices independent of  , and thus they can be easily pre-computed for a simple and fast calculation of  . Also note that the known expression for the Cholesky factor of  , precisely 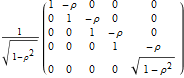 , can be used to implement a fast simulation method for 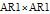 images. [1] J. B. Walsh, "An Introduction to Stochastic Partial Differential Equations," in École d'Été de Probabilités de Saint Flour XIV - 1984 (P. L. Hennequin, ed.), Lecture Notes in Mathematics, vol 1180, Berlin, Heidelberg: Springer, 1984 pp. 265–439. doi:10.1007/BFb0074920. [2] S. Baran and K. Sikolya, "Parameter Estimation in Linear Regression Driven by a Gaussian Sheet," Acta Scientiarum Mathematicarum, 78(3), 2012 pp. 689–713. doi:10.1007/BF03651393. [3] D. Khoshnevisan, Multiparameter Processes: An Introduction to Random Fields, New York: Springer, 2002. [4] D. A. Girard, "Efficiently Estimating Some Common Geostatistical Models by 'Energy–Variance Matching' or Its Randomized 'Conditional–Mean' Versions," Spatial Statistics, 21(Part A), 2017 pp. 1–26. doi:10.1016/j.spasta.2017.01.001. [5] Z. Ying, "Maximum Likelihood Estimation of Parameters under a Spatial Sampling Scheme," The Annals of Statistics, 21(3) 1993 pp. 1567–1590. doi:10.1214/aos/1176349272.
|
