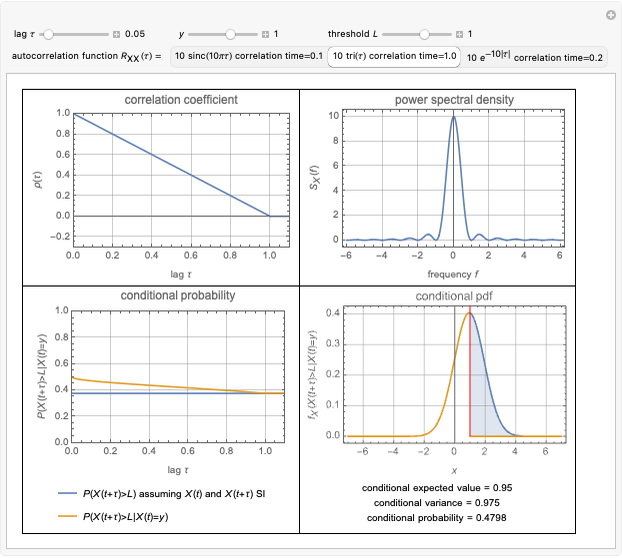
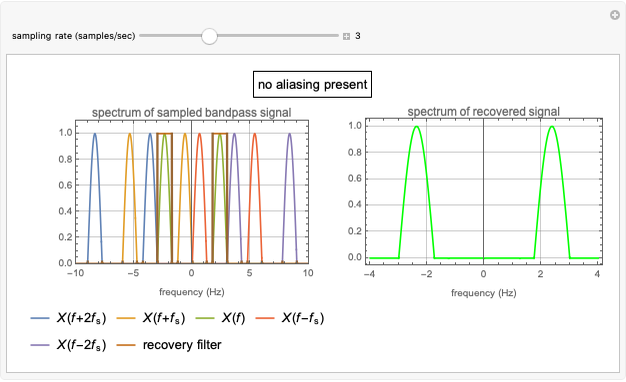
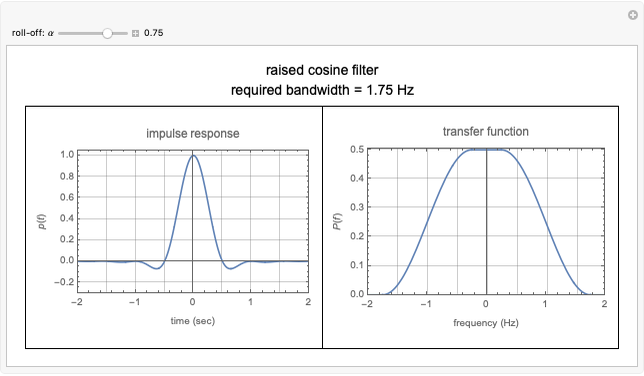
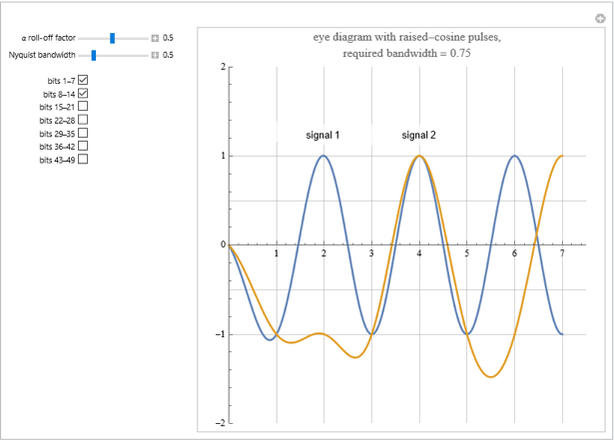
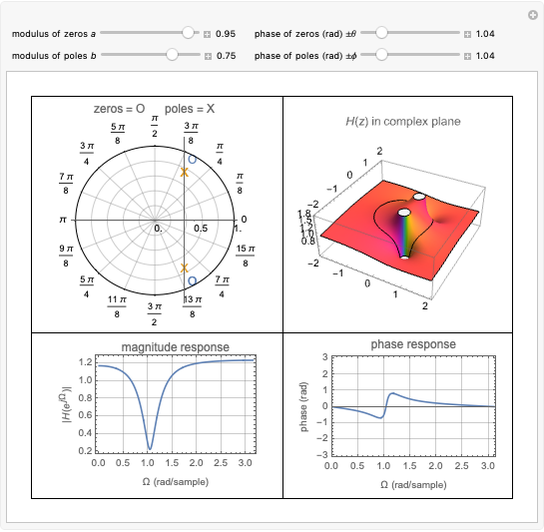
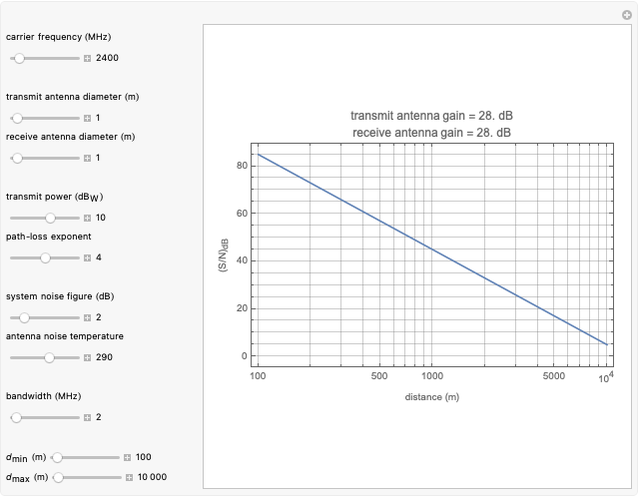
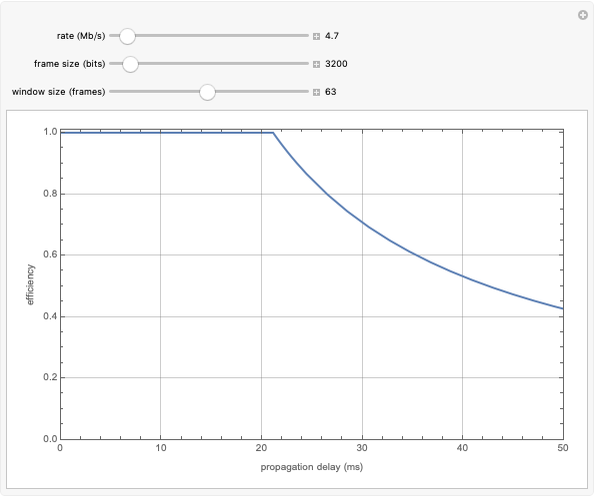
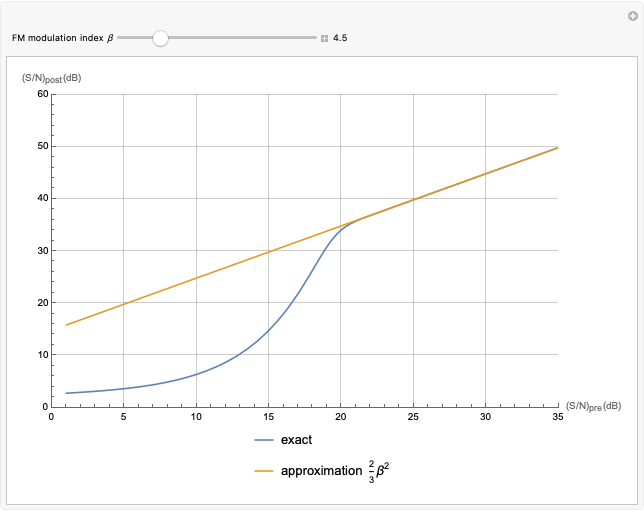
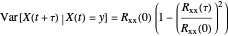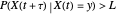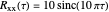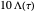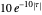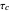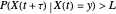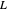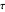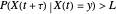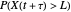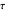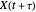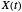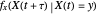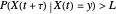Linking Autocorrelation of Gaussian Random Process to Conditional Probabilities
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
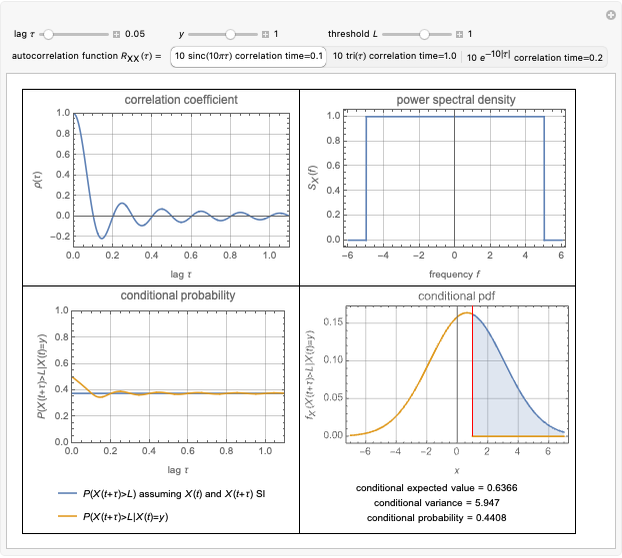
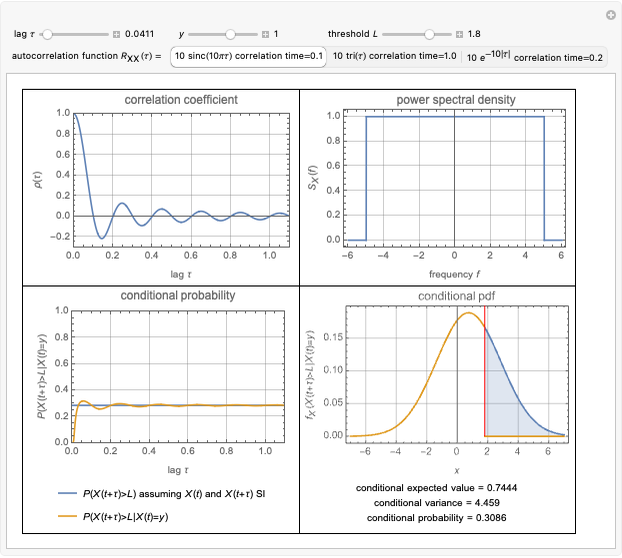
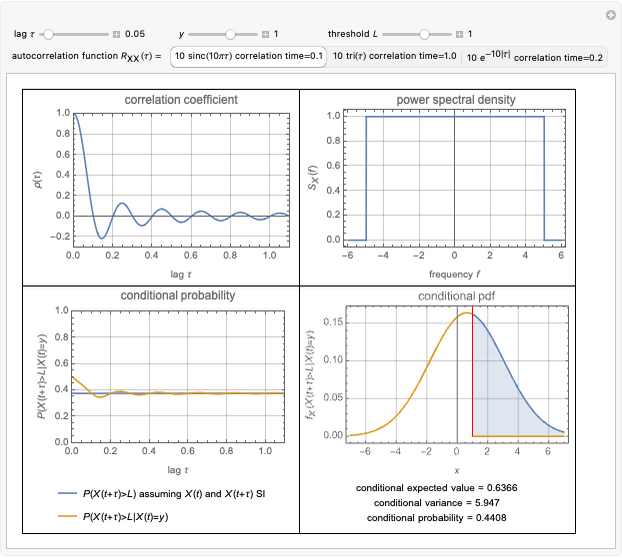
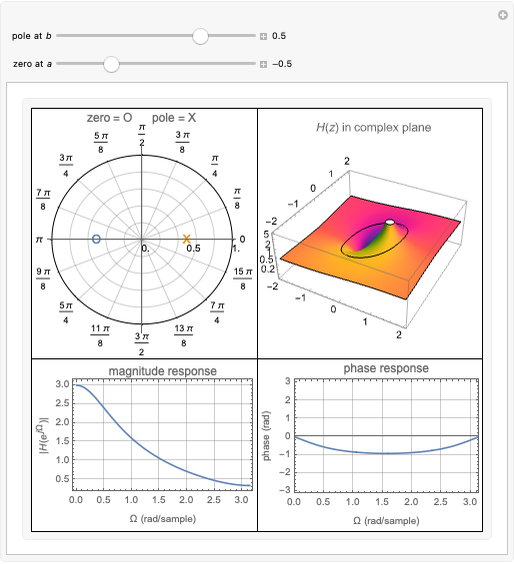
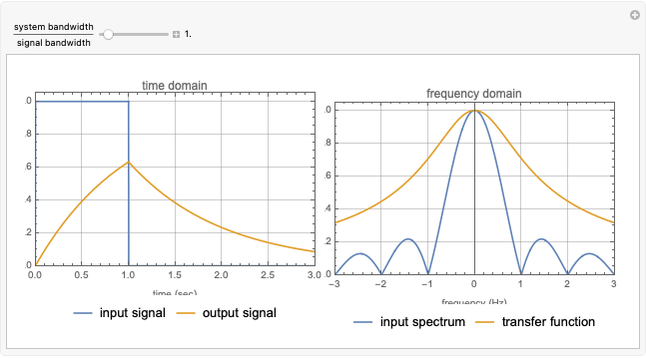
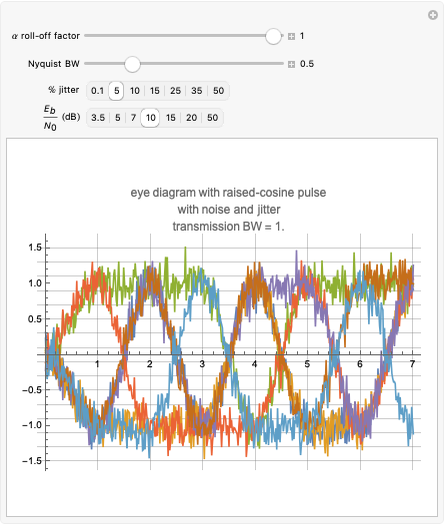
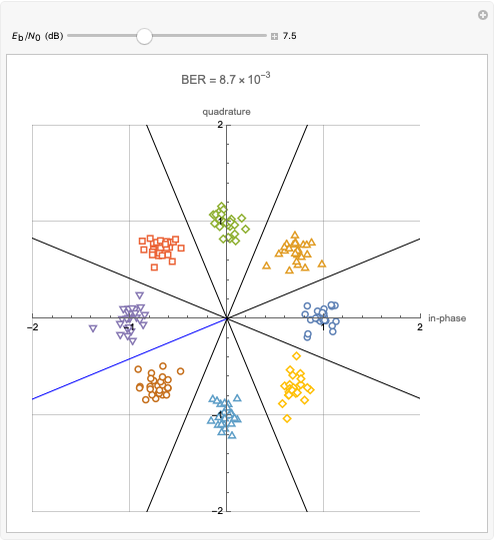
For a zero-mean Gaussian random process 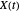 , the probability density function (pdf) of the conditional random variable
, the probability density function (pdf) of the conditional random variable 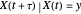 is Gaussian. Its properties can be calculated from the autocorrelation (or power spectral density) of the process,
is Gaussian. Its properties can be calculated from the autocorrelation (or power spectral density) of the process,  (or
(or 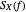 ).
).
Contributed by: Victor S. Frost (October 12)
(University of Kansas)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] K. S. Shanmugan and A. M. Breiphol, Random Signals: Detection, Estimation and Data Analysis, New York: Wiley, 1988.
Snapshots
Permanent Citation