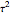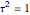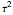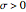Estimating a Centered Ornstein-Uhlenbeck Process under Measurement Errors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
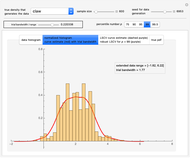
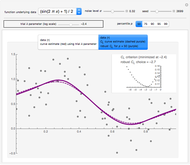
The problem of estimating the two parameters of a stationary process satisfying the differential equation 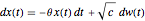 , where
, where  follows a standard Wiener process, from
follows a standard Wiener process, from  observations at equidistant points of the interval
observations at equidistant points of the interval  , has been well studied. This is also the classical problem of fitting an autoregressive time series of order 1 (AR1), the case "
, has been well studied. This is also the classical problem of fitting an autoregressive time series of order 1 (AR1), the case " large" yielding the "near unit root" situation. This Demonstration considers the important case where the observations may have additive measurement errors: we assume that these errors are independent, normal random variables with known variance
large" yielding the "near unit root" situation. This Demonstration considers the important case where the observations may have additive measurement errors: we assume that these errors are independent, normal random variables with known variance 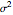 .
.
Contributed by: Didier A. Girard (July 2014)
(CNRS-LJK and Univ. Grenoble Alpes)
Open content licensed under CC BY-NC-SA
Snapshots
Details
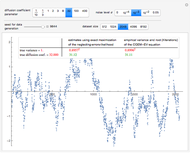
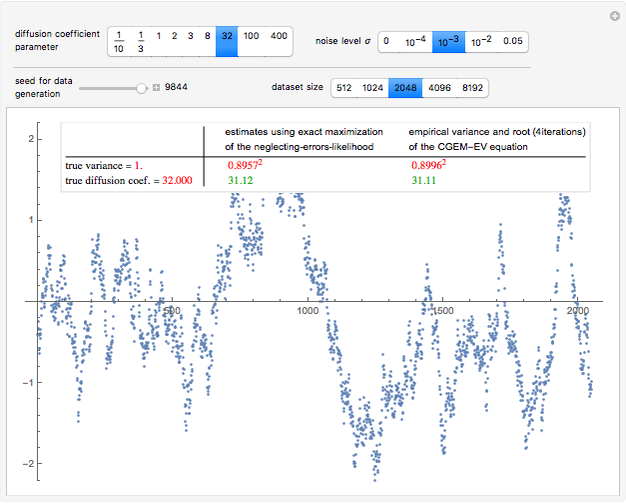
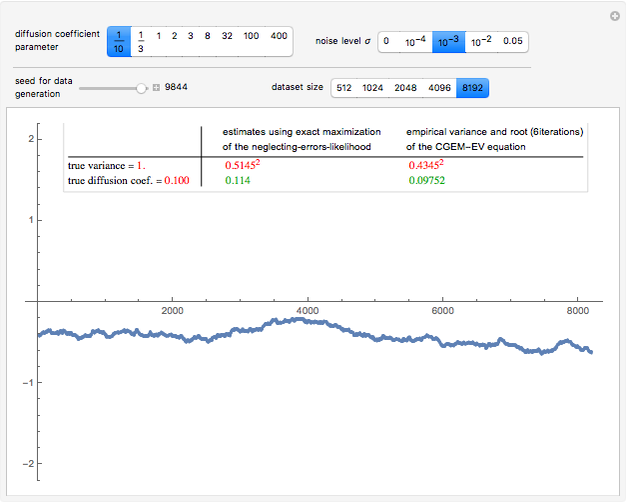
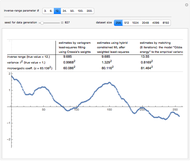
Snapshot 1: Selecting 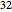 as the true diffusion coefficient (the value of
as the true diffusion coefficient (the value of  from which the non-noisy data is simulated,
from which the non-noisy data is simulated,  being fixed) and choosing
being fixed) and choosing 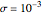 , this setting may be thought of as "close" to a case where the noise could be forgotten; this could be confirmed by moving only
, this setting may be thought of as "close" to a case where the noise could be forgotten; this could be confirmed by moving only  from
from  to
to  (the underlying
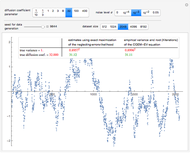
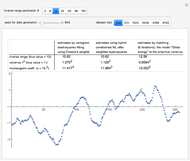
(the underlying 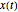 is then unchanged but the measurement errors are eliminated) and observing that all the estimates are almost unchanged (up to three digits). Concerning the diffusion coefficient, you can observe that the two estimation methods produce very close results. Such closeness is less pronounced for the two estimates of the variance. By changing the seed (and thus a new
is then unchanged but the measurement errors are eliminated) and observing that all the estimates are almost unchanged (up to three digits). Concerning the diffusion coefficient, you can observe that the two estimation methods produce very close results. Such closeness is less pronounced for the two estimates of the variance. By changing the seed (and thus a new 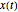 and new measurement errors used to generate the data) you can be convinced that this is not an accident. Furthermore, a rather large variability, from seed to seed, for the two estimates of the variance is also observed; it is much larger than the variability of the estimates of the diffusion coefficient; notice that this observation is well in agreement with the known theory about the estimation of the variance, the inverse-range parameter, and their product (see [1] and the references therein). By moving from seed to seed, neither of the two methods seems a clear winner in this "small noise" setting. Let us now consider a higher noise level. Another important point to note is that the estimates are not very influenced by the noise perturbing the data, provided the noise level stays lower than
and new measurement errors used to generate the data) you can be convinced that this is not an accident. Furthermore, a rather large variability, from seed to seed, for the two estimates of the variance is also observed; it is much larger than the variability of the estimates of the diffusion coefficient; notice that this observation is well in agreement with the known theory about the estimation of the variance, the inverse-range parameter, and their product (see [1] and the references therein). By moving from seed to seed, neither of the two methods seems a clear winner in this "small noise" setting. Let us now consider a higher noise level. Another important point to note is that the estimates are not very influenced by the noise perturbing the data, provided the noise level stays lower than 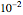 . However, by increasing
. However, by increasing  to 0.05, a clear degradation of the neglecting-errors-ML is observed. In contrast, CGEM-EV still produces reasonable estimates of
to 0.05, a clear degradation of the neglecting-errors-ML is observed. In contrast, CGEM-EV still produces reasonable estimates of  . Here
. Here 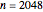 ; however, you can change
; however, you can change  from
from  to
to 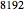 and the conclusions remain similar.
and the conclusions remain similar.
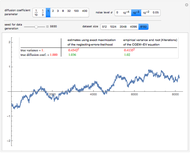
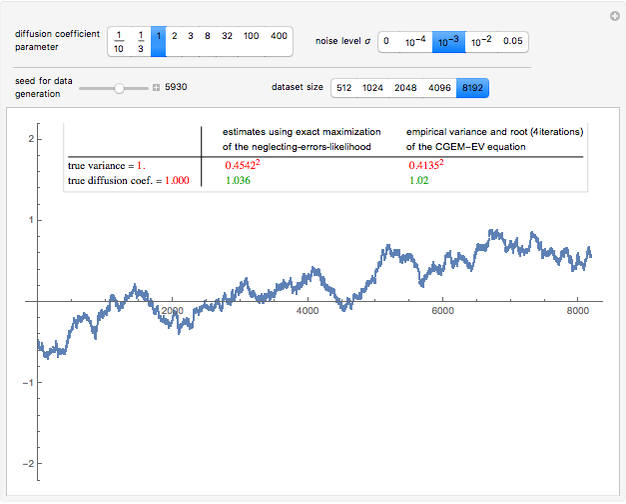
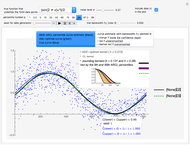
Snapshot 2: Staying at 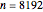 and selecting
and selecting  as true diffusion coefficient (so that we are close to the "near unit root" situation), a noise with
as true diffusion coefficient (so that we are close to the "near unit root" situation), a noise with 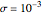 can no longer be considered as a negligible noise. Indeed, we can observe that by diminishing the amplitude of the present noise from
can no longer be considered as a negligible noise. Indeed, we can observe that by diminishing the amplitude of the present noise from  to
to  , we restore significantly the quality of the estimates of
, we restore significantly the quality of the estimates of  using neglecting-errors-ML. And by moving from
using neglecting-errors-ML. And by moving from  to
to  and trying several seeds, one can be convinced that a noise-to-signal ratio of order
and trying several seeds, one can be convinced that a noise-to-signal ratio of order  or less is required if we want to trust the neglecting-errors-ML estimator (since we can be content with three accurate digits in the estimates). By increasing
or less is required if we want to trust the neglecting-errors-ML estimator (since we can be content with three accurate digits in the estimates). By increasing  to 0.05, the neglecting-errors-ML becomes meaningless. In contrast, CGEM-EV still produces reasonable estimates of
to 0.05, the neglecting-errors-ML becomes meaningless. In contrast, CGEM-EV still produces reasonable estimates of  .
.
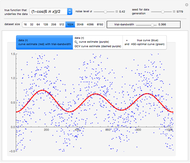
Snapshot 3: Selecting an "intermediate" value  as true diffusion coefficient, similar conclusions can be drawn, except that the approximate upper bound on
as true diffusion coefficient, similar conclusions can be drawn, except that the approximate upper bound on  required to trust the neglecting-errors-ML estimator of
required to trust the neglecting-errors-ML estimator of  seems also intermediate between
seems also intermediate between  and
and  .
.
References
[1] D. A. Girard, "Asymptotic Near-Efficiency of the 'Gibbs-Energy and Empirical-Variance' Estimating Functions for Fitting Matérn Models to a Dense (Noisy) Series." https://hal.archives-ouvertes.fr/hal-00413693.
[2] A. Gloter and J. Jacod, "Diffusions with Measurements Errors, II-Optimal Estimators," ESAIM-Probability and Statistics, 5, 2001 pp. 243–260.
[3] Y. Zhang, H. Yu, and A. Ian McLeod, "Developments in Maximum Likelihood Unit Root Tests," Communications in Statistics—Simulation and Computation, 42(5), 2013 pp. 1088–1103.
Permanent Citation