Confluent Hypergeometric Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The confluent hypergeometric differential equation 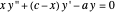 has a regular singular point at
has a regular singular point at  and an essential singularity at
and an essential singularity at  . Solutions analytic at
. Solutions analytic at 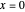 are confluent hypergeometric functions of the first kind (or Kummer functions):
are confluent hypergeometric functions of the first kind (or Kummer functions):
 ,
where
,
where 
 are Pochhammer symbols defined by
are Pochhammer symbols defined by  ,
,  ,
,  . For
. For  , the function becomes singular, unless
, the function becomes singular, unless 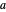 is an equal or smaller negative integer (
is an equal or smaller negative integer ( ), and it is convenient to define the regularized confluent hypergeometric
), and it is convenient to define the regularized confluent hypergeometric  , which is an entire function for all values of
, which is an entire function for all values of  ,
,  and
and  .
The second, linearly independent solutions of the differential equation are confluent hypergeometric functions of the second kind (or Tricomi functions), defined by
.
The second, linearly independent solutions of the differential equation are confluent hypergeometric functions of the second kind (or Tricomi functions), defined by  , where the generalized hypergeometric function
, where the generalized hypergeometric function  represents a formal asymptotic series.
If the hypergeometric function with argument
represents a formal asymptotic series.
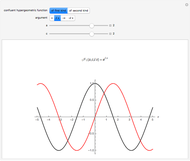
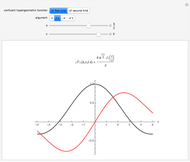
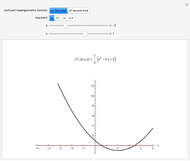
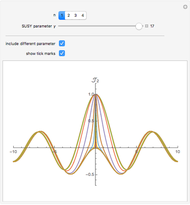
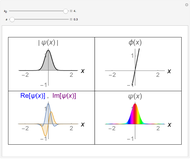
If the hypergeometric function with argument 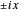 is complex, both the real and imaginary parts are plotted (black and red curves).
For certain choices of the parameters
is complex, both the real and imaginary parts are plotted (black and red curves).
For certain choices of the parameters 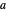 and
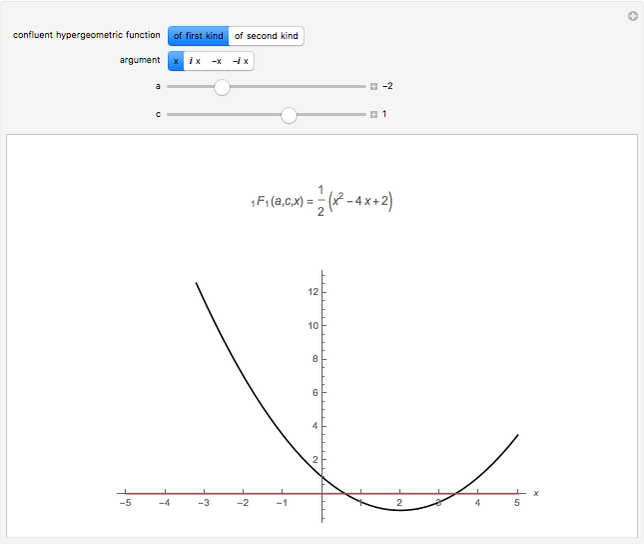
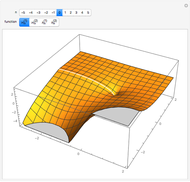
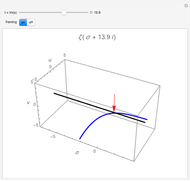
and  , the hypergeometric functions are related to various transcendental and special functions. Several illustrations are given in the snapshots.
, the hypergeometric functions are related to various transcendental and special functions. Several illustrations are given in the snapshots.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
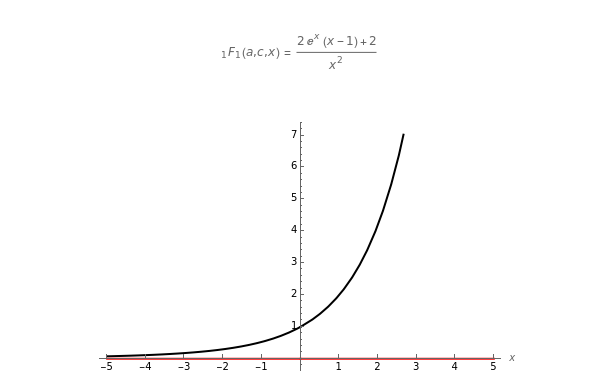
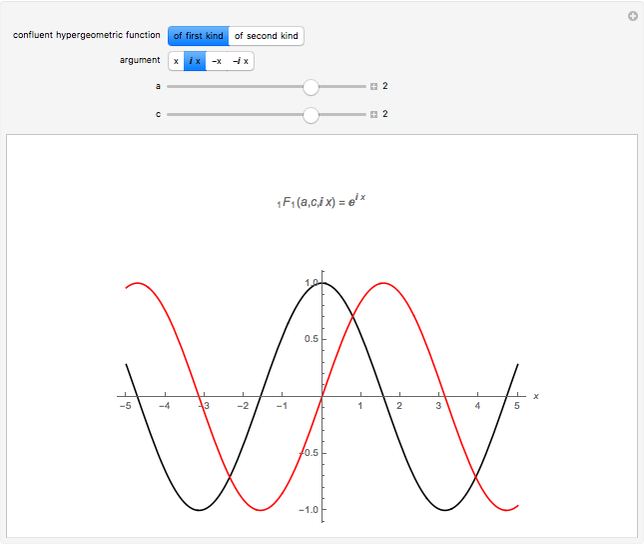
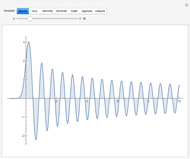
Snapshot 1: when  ,
, 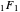 reduces to an exponential function; for example,
reduces to an exponential function; for example,  , for which the real and imaginary parts are plotted
, for which the real and imaginary parts are plotted
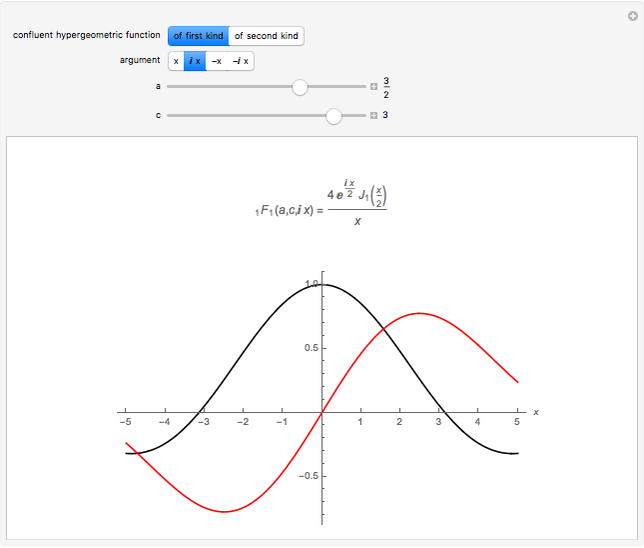
Snapshot 2: relation to Bessel functions: 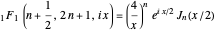
Snapshot 3: Laguerre polynomials: 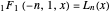
Snapshot 4: error function: 
Snapshot 5: incomplete gamma function: 
Snapshot 6: modified Bessel function: 
Permanent Citation