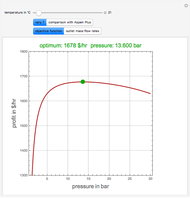
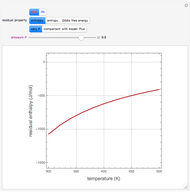
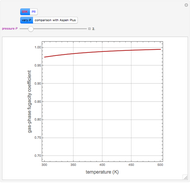
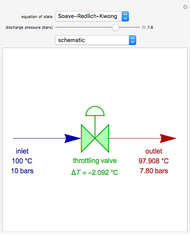
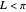Consider a nonlinear partial differential equation that represents the combined effects of diffusion and logistic population growth:
 .
.
Reaction-diffusion equations have been widely applied in the physical and life sciences starting with the pioneering work of Roland Fisher who modeled the spread of an advantageous gene in a population [1]. His model equation, also known as the Fisher–Kolmogorov equation, has the following dimensionless form:
 .
.
The Fisher–Kolmogorov equation is viewed as a prototype for studying reaction-diffusion systems that exhibit bifurcation behavior and traveling wave solutions.
The full mathematical statement of the transient problem is given by the preceding equation with initial condition

and boundary conditions
 ,
,
 .
.
Here  is a dimensionless length for the diffusion zone.
is a dimensionless length for the diffusion zone.
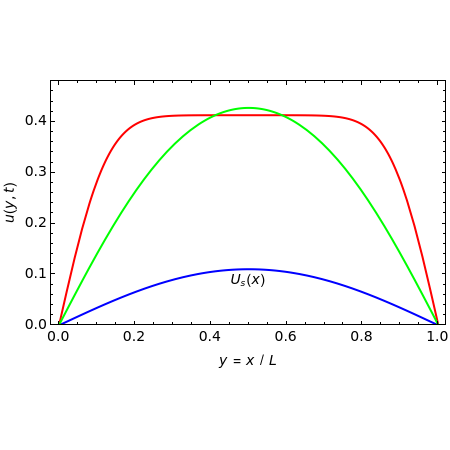
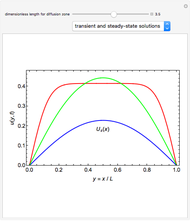
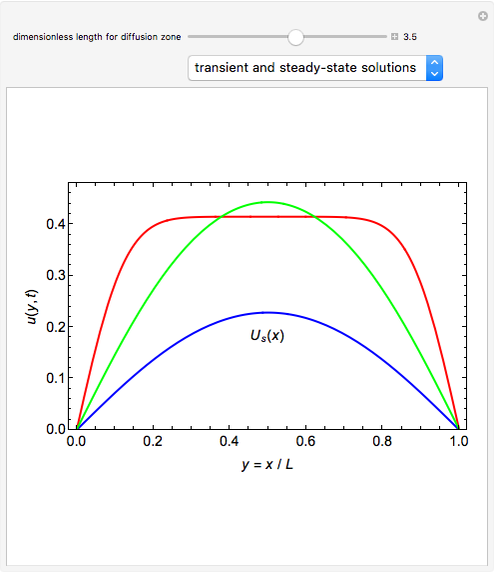
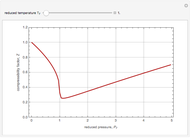
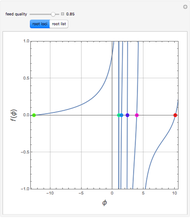
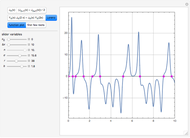
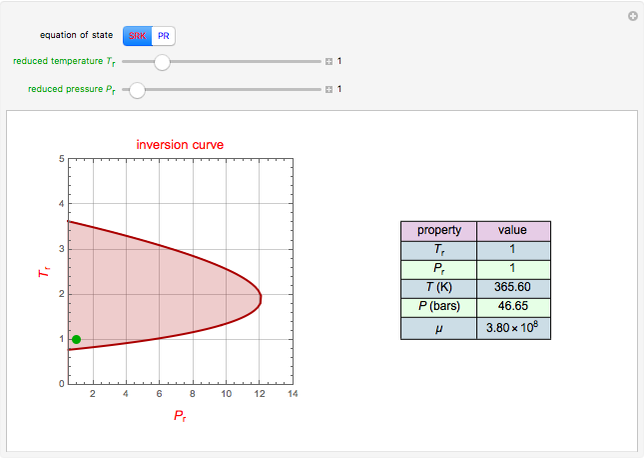
This Demonstration solves this transient reaction-diffusion problem and plots  for
for  equal to 0.005, 0.05, and 60, shown in red, green, and blue, respectively. The steady-state solution
equal to 0.005, 0.05, and 60, shown in red, green, and blue, respectively. The steady-state solution  is obtained for
is obtained for  and is shown in blue. The specified initial condition for the calculations is
and is shown in blue. The specified initial condition for the calculations is  .
.
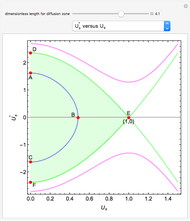
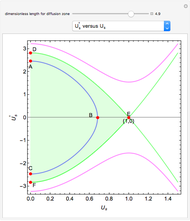
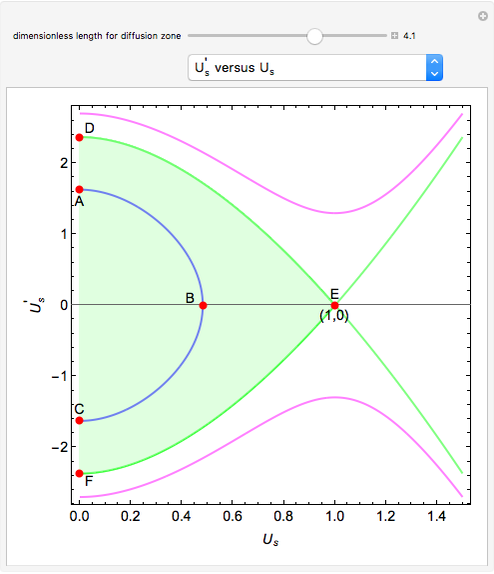
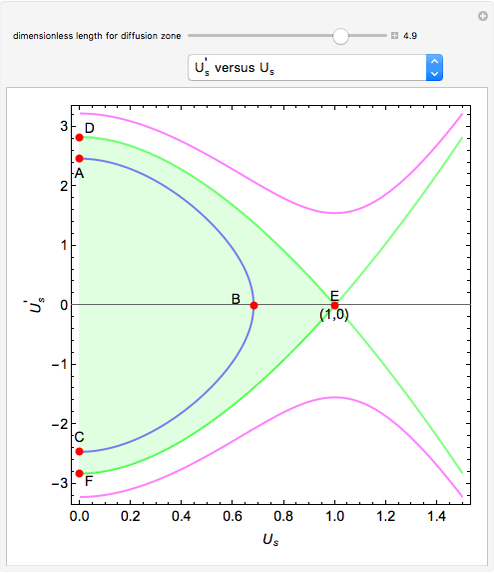
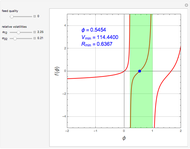
A global stability analysis of the steady states shows that the critical value for  occurs at
occurs at  . Thus for
. Thus for  , the solution is the nontrivial one. For
, the solution is the nontrivial one. For 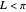 , diffusion stabilizes the steady-state solution
, diffusion stabilizes the steady-state solution  . At the point
. At the point  we have a bifurcation to the nontrivial steady-state solution. This can be readily seen by selecting the
we have a bifurcation to the nontrivial steady-state solution. This can be readily seen by selecting the  versus
versus  plot. The red dot corresponds to the value of
plot. The red dot corresponds to the value of  for the user-set value of
for the user-set value of  .
.
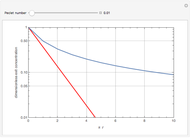
Also shown is the phase plot for the steady solutions, namely,  versus
versus  . The trajectories shown in the phase plot (blue, green, and magenta) are global solutions to the steady-state diffusion equation, but do not necessarily satisfy the boundary conditions. Nontrivial steady-state solutions that satisfy the imposed boundary conditions must lie within the light green region of the phase plot (defined by the orbit
. The trajectories shown in the phase plot (blue, green, and magenta) are global solutions to the steady-state diffusion equation, but do not necessarily satisfy the boundary conditions. Nontrivial steady-state solutions that satisfy the imposed boundary conditions must lie within the light green region of the phase plot (defined by the orbit  . For the user-specified parameters, the orbit
. For the user-specified parameters, the orbit  shown in blue is a feasible nontrivial solution (i.e. for
shown in blue is a feasible nontrivial solution (i.e. for  ).
).
[less]