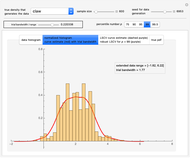
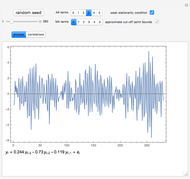
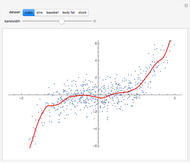
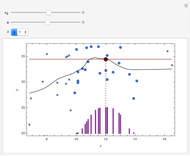
Fitting a Powered Exponential Autocorrelation: Alternatives to Maximum Likelihood via Conjugate Gradient Linear Solvers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
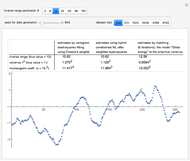
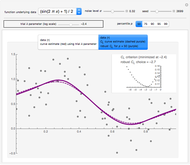
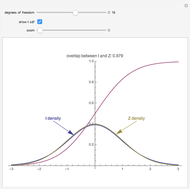
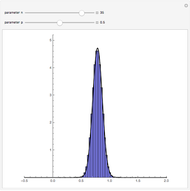
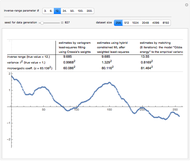
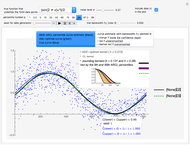
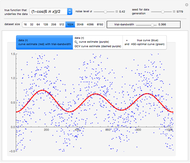
The setting here is the same as described in [1], except that the autocorrelation function, which was the Matérn function, is now replaced by the powered exponential autocorrelation. For the definition of these correlations, see the documentation of the function VariogramModel.
[more]
Contributed by: Didier A. Girard (August 2022)
(CNRS-LJK and Université Grenoble Alpes)
Open content licensed under CC BY-NC-SA
Snapshots
Details
See further details and references in [1].
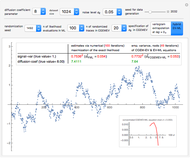
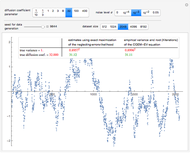
The computation of  , where
, where  , still uses a conjugate-gradient (CG) solver preconditioned by the classical factored sparse approximate inverse (FSAI) method, each product by
, still uses a conjugate-gradient (CG) solver preconditioned by the classical factored sparse approximate inverse (FSAI) method, each product by  being obtained via FFTs from the standard embedding of
being obtained via FFTs from the standard embedding of  in a circulant
in a circulant  matrix.
matrix.
References
[1] D. A. Girard, "Estimating a Centered Matérn (1) Process: Three Alternatives to Maximum Likelihood via Conjugate Gradient Linear Solvers" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/EstimatingACenteredMatern1ProcessThreeAlternativesToMaximumL.
[2] N. Cressie, "Fitting Variogram Models by Weighted Least Squares," Journal of the International Association for Mathematical Geology, 17(5), 1985 pp. 563–586. doi:10.1007/BF01032109.
[3] H. Zhang and D. L. Zimmerman, "Hybrid Estimation of Semivariogram Parameters," Mathematical Geology, 39(2), 2007 pp. 247–260. doi:10.1007/s11004-006-9070-8.
[4] D. A. Girard, "Asymptotic Near-Efficiency of the 'Gibbs-Energy and Empirical-Variance' Estimating Functions for Fitting Matérn Models to a Dense (Noisy) Series." arxiv.org/abs/0909.1046v2.
[5] E. Anderes, "On the Consistent Separation of Scale and Variance for Gaussian Random Fields," The Annals of Statistics, 38(2), 2010 pp. 870–893. doi:10.1214/09-AOS725.
[6] W.-Li. Loh, "Estimating the Smoothness of a Gaussian Random Field from Irregularly Spaced Data via Higher-Order Quadratic Variations," The Annals of Statistics, 43(6), 2015 pp. 2766–2794. doi:10.1214/15-AOS1365.
Permanent Citation